Hypotenuse and height
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- planimetrics
- right triangle
- triangle
- The right triangle altitude theorem
- numbers
- real numbers
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Rectangle
 In rectangle ABCD with sides, |AB|=19, |AD|=16 is from point A guided perpendicular to the diagonal BD, which intersects at point P. Determine the ratio (|PB|)/(|DP|).
In rectangle ABCD with sides, |AB|=19, |AD|=16 is from point A guided perpendicular to the diagonal BD, which intersects at point P. Determine the ratio (|PB|)/(|DP|). - Right Δ
 A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle.
A right triangle has the length of one leg 72 cm and the hypotenuse 90 cm size. Calculate the height of the triangle. - Area of RT
 Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5.
Calculate the right triangle area that hypotenuse has length 14, and one hypotenuse segment has length 5. - Area of RT
 The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
The right triangle has orthogonal projections of legs to the hypotenuse lengths 15 cm and 9 cm. Determine the area of this triangle.
- Euclid1
 The right triangle has hypotenuse c = 27 cm. How large sections cuts height hc=3 cm on the hypotenuse c?
The right triangle has hypotenuse c = 27 cm. How large sections cuts height hc=3 cm on the hypotenuse c? - No problem
 No problem; here are five decimal addition problems for you to practice: 1. What is the result of 3.5 + 2.1? 2. What is the result of 0.8 + 0.3? 3. What is the result of 5.2 + 1.7? 4. What is the result of 2.5 + 0.9? 5. What is the result of 1.4 + 0.6? I
No problem; here are five decimal addition problems for you to practice: 1. What is the result of 3.5 + 2.1? 2. What is the result of 0.8 + 0.3? 3. What is the result of 5.2 + 1.7? 4. What is the result of 2.5 + 0.9? 5. What is the result of 1.4 + 0.6? I - Decadic number
 What is the expanded form of this number? 18.029 A: (1x10)+(8x1)+(2x1/10)+(9x1/100) B: (1×10)+(8×1)+(2×1/10)+(9×1/1,000) C: (1×10)+(8×1)+(2×1/100)+(9×1/1,000) D: (1×10)+(8×1)+(2×11/00)+(9×1/100)
What is the expanded form of this number? 18.029 A: (1x10)+(8x1)+(2x1/10)+(9x1/100) B: (1×10)+(8×1)+(2×1/10)+(9×1/1,000) C: (1×10)+(8×1)+(2×1/100)+(9×1/1,000) D: (1×10)+(8×1)+(2×11/00)+(9×1/100) - Scientific notation mul
 A student found the product of 8 × 10³ and 7 × 105 to be 5.6 × 108. What is the error? What is the correct product? Complete the explanation.
A student found the product of 8 × 10³ and 7 × 105 to be 5.6 × 108. What is the error? What is the correct product? Complete the explanation. - Jacqui
 Jacqui ran a mile and a half on Monday, Wednesday, and Friday and three-fourths of a mile on Tuesday and Thursday. How far did she run in all?
Jacqui ran a mile and a half on Monday, Wednesday, and Friday and three-fourths of a mile on Tuesday and Thursday. How far did she run in all?
- James 7
 James bought a pair of shoes worth 650.00 pesos. Eyeglasses that cost p 86.75 and some school supplies worth p 538.95. How much did he spend in all?
James bought a pair of shoes worth 650.00 pesos. Eyeglasses that cost p 86.75 and some school supplies worth p 538.95. How much did he spend in all? - During 2
 During the 2006 Olympics, a gymnast received the following scores: 8.9, 9.2, 9.15, and 9.05. What is the sum of the gymnast's scores?
During the 2006 Olympics, a gymnast received the following scores: 8.9, 9.2, 9.15, and 9.05. What is the sum of the gymnast's scores? - Evaluate expression
 What is: the sum of negative four and one-half times n plus the quantity one-fourth plus one and three-fourths times n minus three-eighths?
What is: the sum of negative four and one-half times n plus the quantity one-fourth plus one and three-fourths times n minus three-eighths? - What is 21
 What is the next number? What is the 7th number? 160, 80, 40, 20, 10, _
What is the next number? What is the 7th number? 160, 80, 40, 20, 10, _ - Quadrilateral 78874
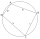 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
- Sum of absolute values
 Is it possible for |r| + |s| = |r+s|? If so, when?
Is it possible for |r| + |s| = |r+s|? If so, when? - Overnight change
 It was 13°C yesterday, but the temperature changed by -18.6° overnight. What is the temperature now?
It was 13°C yesterday, but the temperature changed by -18.6° overnight. What is the temperature now? - Recycling center
 Pavani collects 20.3 pounds of metal to take to a recycling center. The recycling center pays her for 18.4 pounds of the metal and refuses the rest of it. How much of Pavani's collection was refused, in pounds? Enter your answer as a decimal, if necessary
Pavani collects 20.3 pounds of metal to take to a recycling center. The recycling center pays her for 18.4 pounds of the metal and refuses the rest of it. How much of Pavani's collection was refused, in pounds? Enter your answer as a decimal, if necessary
