ABCD
AC= 40cm , angle DAB=38 , angle DCB=58 , angle DBC=90 , DB is perpendicular on AC , find BD and AD
Correct answer:

Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
Cosine rule uses trigonometric SAS triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- planimetrics
- right triangle
- triangle
- The Law of Cosines
- The Law of Sines
- goniometry and trigonometry
- sine
- cosine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Isosceles 83157
 Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α.
Using the cosine theorem, prove that in an isosceles triangle ABC with base AB, c=2a cos α. - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
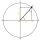 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Using 4
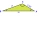 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A right
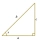 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - A triangle 7
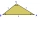 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Felix
 Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km.
Calculate how much land Felix Baumgartner saw after jumping from 36 km above the ground. The radius of the Earth is R = 6378 km. - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Solve 13
 Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a
Solve the missing dimensions for the following triangle: Triangle ABC: AngleA=43 degrees, b=7.0cm, c=6.0cm Question 1. Angle B with units written as degrees Question 2. Angle C with units written as degrees Question 3. a, rounded to the nearest tenth of a - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
