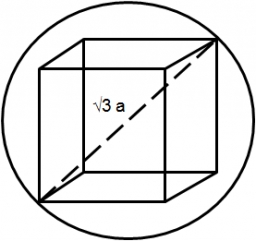
Cube in a sphere
The cube is inscribed in a sphere with a volume 7253 cm3. Determine the length of the edges of a cube.
Correct answer:
Showing 3 comments:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
The Pythagorean theorem is the base for the right triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- arithmetic
- cube root
- square root
- division
- solid geometry
- cube
- sphere
- space diagonal
- planimetrics
- Pythagorean theorem
- numbers
- fractions
- real numbers
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Annual interest
 A loan of 10 000 euros is to be repaid in annual payments over ten years. Assuming a fixed 10% annual interest rate compounded annually, calculate: (a) the amount of each annual repayment (b) the total interest paid.
A loan of 10 000 euros is to be repaid in annual payments over ten years. Assuming a fixed 10% annual interest rate compounded annually, calculate: (a) the amount of each annual repayment (b) the total interest paid. - Infinite sum of areas
 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Infinite decimal
 Imagine the infinite decimal number 0.99999999... That is a decimal and her endless series of nines. Determine how much this number is less than the number 1. Thank you in advance.
Imagine the infinite decimal number 0.99999999... That is a decimal and her endless series of nines. Determine how much this number is less than the number 1. Thank you in advance. - Series and sequences
 Find a fraction equivalent to the recurring decimal. 0.435643564356
Find a fraction equivalent to the recurring decimal. 0.435643564356
- Decimal to fraction
 Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures.
Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures. - Fraction
 Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator.
Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator. - Sum of series
 Determine the 6-th member and the sum of a geometric series: 5-4/1+16/5-64/25+256/125-1024/625+....
Determine the 6-th member and the sum of a geometric series: 5-4/1+16/5-64/25+256/125-1024/625+.... - Closer to one
Here are two sums: A=1/2 + 1/3 and B=1/5 + 1/3. Which of the two sums is closer in value to 1? You must show your work and state clearly whether the answer is A or B.
- NYC block
 Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block
Bijan wants to go running during his family's vacation to New York City. To do so, he will run a neighborhood block 20 times. Bijan runs a total of 8 miles. The block has a length of 3/20 miles. Use the formula for the perimeter of the neighborhood block
- Richard
 Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number?
Richard is conducting an experiment. Every time he flips a fair two-sided coin, he also rolls a six-sided die. What is the probability that the coin will land on tails and the die will land on an even number? - Locker combination
 Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly?
Todd forgot the first two numbers of his locker combination. The numbers can be any number 1 through 6. What is the probability that he will guess the first number correctly and the second number incorrectly? - Multiply mixed
 What is six-eighths times five? Your answer should be in mixed number form. Some hints: one and ten-thirtieths three and six-eighths six and four-sixths nine and three-fifths
What is six-eighths times five? Your answer should be in mixed number form. Some hints: one and ten-thirtieths three and six-eighths six and four-sixths nine and three-fifths - Mixed numbers equation
 4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box.
4 5/9 is the same as the sum of 2 1/3 and 5/6 times a number. What is the number? Enter your answer as a mixed number in simplest form in the box. - Saravanan
 Saravanan's father bought 2 3/4 m, 2 1/2 m, and 1 1/4 m of cloth. What was the total length of the cloth he bought?
Saravanan's father bought 2 3/4 m, 2 1/2 m, and 1 1/4 m of cloth. What was the total length of the cloth he bought?
- Negative mixed number 2
 What is the product of 1 1/2 and -1 1/4? Enter your answer as a mixed number, in simplest form, in the box.
What is the product of 1 1/2 and -1 1/4? Enter your answer as a mixed number, in simplest form, in the box. - Monthly expenses
 John's monthly expenses are analyzed as follows: 1/8 for stationery, 1/3 for fuel, 1/6 for parking, and the rest for food. His total expenses are 4500. Calculate the rand value of the food expenses.
John's monthly expenses are analyzed as follows: 1/8 for stationery, 1/3 for fuel, 1/6 for parking, and the rest for food. His total expenses are 4500. Calculate the rand value of the food expenses. - 13 times
 1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box.
1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box.
