Equation of circle 2
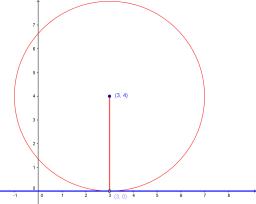
Find the equation of a circle that touches the axis of y at a distance of 4 from the origin and cuts off an intercept of length 6 on the axis x.
Result
Result
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Collinear lines
 Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC?
Points A, B, and C are collinear, and B lies between A and C. If AC = 48, AB = 2x + 2, and BC = 3x + 6, what is BC? - The endpoints
 The endpoints of a segment are (-6,1) and (10,11). What are the coordinates of its midpoint?
The endpoints of a segment are (-6,1) and (10,11). What are the coordinates of its midpoint? - Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - There 35
 There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
There are three points on a straight line: A, BC. If CD = 8x, DE = 3, and CE = x + 10, what is CD? Simplify your answer and write it as a proper fraction, mixed number, or integer.
- Line equation:
 Line equation: y-3=8/9(x-5) Solve for slope
Line equation: y-3=8/9(x-5) Solve for slope - The slope 2
 What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form.
What is the slope of the line that passes through the points (-4, -7) and (-2,-19)? Write your answer in the simplest form. - A 100-inch
 A 100-inch stick is to be divided into four using the ratio 2: 5: 7: 11. How long is the longest piece?
A 100-inch stick is to be divided into four using the ratio 2: 5: 7: 11. How long is the longest piece? - Line segment
 Find the length of the line joining points A(-4,8) and B(-1,4).
Find the length of the line joining points A(-4,8) and B(-1,4). - Midpoint between conjugate
 Find the midpoint between two roots: 2+3.464i and 2 - 3.464i
Find the midpoint between two roots: 2+3.464i and 2 - 3.464i
- Slope of line
 What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)?
What is the slope of the line that passes through the points: (-2, 4) and (-3, 1)? - Midpoint of line segment
 Find the midpoint of the line segment joining the points (10,1) and (-8,-1).
Find the midpoint of the line segment joining the points (10,1) and (-8,-1). - The midpoint 2
 Find the value of x if M is the midpoint of PQ, PQ=10x−7, and PM=14.
Find the value of x if M is the midpoint of PQ, PQ=10x−7, and PM=14. - Polygon 3
 Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation?
Polygon ABCD is dilated, rotated, and translated to form polygon QWER. The endpoints A and B are at (0, -7) and (8, 8), and the endpoints QW are at (6, -6) and (2, 1.5). What is the scale factor of the dilation? - Divide line segment
 Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
Find the point P on line segment AB, such that |AP| = r |AB|. Coordinates of endpoints: A = (−2, 0, 1), B = (10, 8, 5), ratio r = 1/4.
- Trapezoid 70454
 Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60°
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Lengths 69314
 We must cut three steel bars with 24 dm, 3 m, and 160 cm lengths into equal lengths. Find their maximum length and number.
We must cut three steel bars with 24 dm, 3 m, and 160 cm lengths into equal lengths. Find their maximum length and number. - Enlarge 66284
 We will enlarge the line 8 cm long in the ratio of 7:4. How long in cm will the new line be?
We will enlarge the line 8 cm long in the ratio of 7:4. How long in cm will the new line be?
