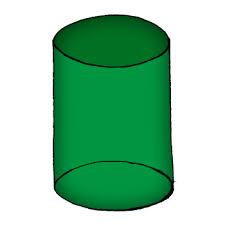
Cylindrical container
An open-topped cylindrical container has a volume of V = 3140 cm3. Find the cylinder dimensions (radius of base r, height v) so that the least material is needed to form the container.
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Tent - spherical cap
 I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What
I have a tent in the shape of a spherical cap. Assume we want the volume to be 4 cubic meters, to sleep two or three people. Assume that the material making up the dome of the ten is twice as expensive per square as the material touching the ground. What - Dogde Caliber
 The petrol kilometers M (unit: kilometers per liter) of the Dodge Caliber car is modeled by the function: M(s) = - 1/28s² + 3s- 31 What is the car's best petrol kilometers, and what speed is attained?
The petrol kilometers M (unit: kilometers per liter) of the Dodge Caliber car is modeled by the function: M(s) = - 1/28s² + 3s- 31 What is the car's best petrol kilometers, and what speed is attained? - Use L
 Use L Hospital's rule to solve (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii)Lim x³+x²-x-1/x²-2x-3 X—>3
Use L Hospital's rule to solve (i) Lim x²+5x-14/x²-5x+6 X—>2 (ii)Lim x³+x²-x-1/x²-2x-3 X—>3 - A particle 2
 If the motion of a particle is described by the relation a(t) = 7t³ + 2 m/s², and the initial velocity of the motion is zero when t = 0 and the distance is 2m, t = 0.5s. Determine the velocity and displacement when t = 10s.
If the motion of a particle is described by the relation a(t) = 7t³ + 2 m/s², and the initial velocity of the motion is zero when t = 0 and the distance is 2m, t = 0.5s. Determine the velocity and displacement when t = 10s.
- Parabola with abs
 A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x)
A). Sketch the graph of the function f(x)=x * absolute(x) = x * |x| b). For what values of x is f(x) differentiable c). Find F(x) - Intersection of Q2 with line
 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - Function x*tanx
 Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph.
Functions: f(x)=xtanx f(x)=(e^x)/((e^x)+1) Find; i)vertical and horizontal asymptotes iii)the interval of decrease and increase iii)Local maxima and local minima iv)interval of concavity and inflection. And sketch the graph. - The MRT train
 The MRT running from Taft to North Avenue has a starting velocity of 60km/hr. After a malfunction, the brakes failed, making the train run at a velocity of 80km/hr. What is the acceleration rate if the time for velocity change is 5 seconds?
The MRT running from Taft to North Avenue has a starting velocity of 60km/hr. After a malfunction, the brakes failed, making the train run at a velocity of 80km/hr. What is the acceleration rate if the time for velocity change is 5 seconds? - Penny free fall
 A man drops a penny from the top of a 500m tall building. After t seconds, the penny has fallen a distance of s meters, where s(t)=500-5t². Determine the average velocity between 1s and 5s.
A man drops a penny from the top of a 500m tall building. After t seconds, the penny has fallen a distance of s meters, where s(t)=500-5t². Determine the average velocity between 1s and 5s.
- Martians
 A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal?
A sphere-shaped spaceship with a diameter of 6 m landed in the meadow. To avoid attracting attention, the Martians covered it with a roof in the shape of a regular cone. How high will this roof be so that the consumption of roofing is minimal? - Megapizza
 Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion?
Mega pizza will be divided among 100 people. First gets 1%, 2nd 2% of the remainder, 3rd 3% of the remainder, etc. Last 100th 100% of the remainder. Which person got the biggest portion? - Sleep vs. watch TV time
 Using a data set relating to the number of episodes I watch on TV in a day (x) versus the number of hours of sleep I get that night (y), I construct the linear model y=−0.6x+11 Which of the following general observations can you make from this model? a) I
Using a data set relating to the number of episodes I watch on TV in a day (x) versus the number of hours of sleep I get that night (y), I construct the linear model y=−0.6x+11 Which of the following general observations can you make from this model? a) I - Ascend vs. descent
 Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2
Which function is growing? a) y = 2-x b) y = 20 c) y = (x + 2). (-5) d) y = x-2 - Maximum of volume
 The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
- The shooter
 The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stop firing. (a) What is the most likely num
The shooter shoots at the target, assuming that the individual shots are independent of each other and the probability of hitting them is 0.2. The shooter fires until he hits the target for the first time, then stop firing. (a) What is the most likely num - Derivative problem
 The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal.
The sum of two numbers is 12. Find these numbers if: a) The sum of their third powers is minimal. b) The product of one with the cube of the other is maximal. c) Both are positive, and the product of one with the other power of the other is maximal. - Shopping malls
 The chain of department stores plans to invest up to 24,000 euros in television advertising. Ads will place all commercials on a television station where the broadcast of a 30-second spot costs EUR 1,000 and is watched by 14,000 potential customers. Durin
The chain of department stores plans to invest up to 24,000 euros in television advertising. Ads will place all commercials on a television station where the broadcast of a 30-second spot costs EUR 1,000 and is watched by 14,000 potential customers. Durin
