Coffee
In-stock are three kinds of branded coffee prices:
I. Kind. .. .. .205 Kc/kg
II. Kind. .. .. .274 Kc/kg
III. Kind. .. .. 168 Kc/kg
Mixing these three species in the ratio 8:5:6 create a mixture. What will be the price of 100 grams of this mixture?
I. Kind. .. .. .205 Kc/kg
II. Kind. .. .. .274 Kc/kg
III. Kind. .. .. 168 Kc/kg
Mixing these three species in the ratio 8:5:6 create a mixture. What will be the price of 100 grams of this mixture?
Correct answer:

Tips for related online calculators
Looking for a statistical calculator?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
- statistics
- weighted average
- algebra
- equation
- system of equations
- arithmetic
- multiplication
- division
- addition
- basic functions
- direct relationship
- numbers
- rational numbers
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - Circumferences 83111
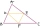 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Cupcakes
 Keia and Hiro made a total of 27 cupcakes. Keia made 2 times as many cupcakes as Hiro. How many cupcakes did Hiro make?
Keia and Hiro made a total of 27 cupcakes. Keia made 2 times as many cupcakes as Hiro. How many cupcakes did Hiro make? - Violin and dance lesson
 Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of
Each week, Nina takes a violin lesson and a dance lesson. The dance lesson costs ⅔ as much as the violin lesson, and the combined cost is $75. Which systems of equations could be used to find d, the cost of the dance lesson in dollars, and v, the cost of - Addition method
 Solve for the variables by substitution or addition method: x + 3y = 19 5x + 3y = 35
Solve for the variables by substitution or addition method: x + 3y = 19 5x + 3y = 35 - Vertex of the rectangle
 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Dostaneli
 If we get 5% of the amount that Petr has in his wallet and 4% of the amount that Paul has with him, we will have 46 CZK. However, if we get 4% from Peter's and 5% from Paul's, we will only have 44 CZK. How many crowns do Petr and Paul have with them?
If we get 5% of the amount that Petr has in his wallet and 4% of the amount that Paul has with him, we will have 46 CZK. However, if we get 4% from Peter's and 5% from Paul's, we will only have 44 CZK. How many crowns do Petr and Paul have with them? - Department 82388
 Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart
Last year, there were 30 more boys than girls in our scout troop. This year, the number of children in the ward increased by 10%, while the number of boys increased by 5% and the number of girls increased by 20%. How many children do we have in the depart - Three equations
 Find the solution to the equations x-y+z=-1 x+y+3z=-3 2x-y+2z=0
Find the solution to the equations x-y+z=-1 x+y+3z=-3 2x-y+2z=0 - Calculate 415
 Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm².
Calculate the cuboid's dimensions if the sum of its edges is 19cm. The body's diagonal size is 13 cm, and its volume is 144 cm³. The total surface area is 192 cm². - Two containers 2
 Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on
Two containers, one large and one small, contain a total of 4 kilograms of bath salts. One-quarter of the bath salts from the large container are transferred to the small container, so the ratio of bath salts in the large container to that in the small on - Third unknown number
 The number A is 5 more than the number C and 10 less than the number B. The sum of A+B=100. What is the C number?
The number A is 5 more than the number C and 10 less than the number B. The sum of A+B=100. What is the C number? - The sum 40
 The sum of the two numbers is 75. If the smaller number is 20 more than 1/5 of the larger number, find those two numbers. The large number is x, and the small number is y.
The sum of the two numbers is 75. If the smaller number is 20 more than 1/5 of the larger number, find those two numbers. The large number is x, and the small number is y. - Flower shop
 In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost
In a flower shop, a bunch containing 3 tulips, 2 roses, and 1 daffodil cost $10.79. A different bunch containing 1 tulip, 2 roses, and 3 daffodils costs $10.13. A tulip costs 35 cents more than a rose. How much does 1 tulip and 1 rose, and 1 daffodil cost
