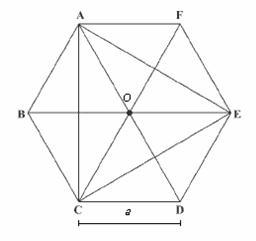
Hexagon ABCDEF
In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
- algebra
- expression of a variable from the formula
- planimetrics
- right triangle
- polygon
- area of a shape
- perimeter
- triangle
- diagonal
- goniometry and trigonometry
- arcsine
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²? - The rectangle 5
 The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r
The rectangle OABC has one vertex at O, the center of a circle, and a second vertex A is 2 cm from the edge of the circle, as shown. The vertex A is also a distance of 7 cm from C. The point B and C lie on the circumference of the circle. a. What is the r - A rhombus 4
 A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution.
A rhombus has a side length of 10 cm. Find the angles at each corner of the rhombus if the shorter of the two diagonals measures 7 cm. Give your answers to the nearest degree and give clear geometric reasoning at each stage of your solution. - The diagonal 4
 The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter.
The diagonal of a rhombus measures 16 cm and 30 cm. Find its perimeter. - Consider 3
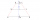 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - Rectangular 63094
 Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long.
Calculate the perimeter and the area of a rectangular garden if the diagonal length is 18 m long and one of the sides of the garden is 9m long. - The diagonals
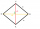 The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond?
The diagonals in the diamond ABCD are 6 cm and 8 cm long. What is the perimeter of this diamond? - Side wall planes
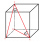 Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls.
Find the volume and surface of a cuboid whose side c is 30 cm long and the body diagonal forms angles of 24°20' and 45°30' with the planes of the side walls. - A prism
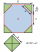 A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism.
A prism with an altitude of 15cm has a base in the form of a regular octagon inscribed in a square of 10cmx10cm. Find the volume of the prism. - Octahedron in a cube
 What largest octahedron can we place inside a cubical box with sides equal to 72?
What largest octahedron can we place inside a cubical box with sides equal to 72? - How long
 How long is the diagonal of the square with side a = 50mm?
How long is the diagonal of the square with side a = 50mm? - Turning machine
 What is the smallest diameter of the cylinder so that a square prism with a side of 40 cm can be turned from it?
What is the smallest diameter of the cylinder so that a square prism with a side of 40 cm can be turned from it? - Trapezoid and diagonals
 Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm.
Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm. - The block
 The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block.
The block has dimensions of 5 cm, 10 cm, and 15 cm. Calculate the size of the wall diagonals of this block. - A paint
 A paint tin is a cylinder of 12cm and a height of 22 cm. Leonardo, the painter, drops his stirring stick into the tin, and it disappears. Work out the maximum length of the stick.
A paint tin is a cylinder of 12cm and a height of 22 cm. Leonardo, the painter, drops his stirring stick into the tin, and it disappears. Work out the maximum length of the stick. - Diagonals of rhombus
 Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm.
Find the length of the diagonal AC of the rhombus ABCD if its perimeter P = 112 dm and the second diagonal BD has a length of 36 dm. - One of
 One of the internal angles of the rhombus is 120°, and the shorter diagonal is 3.4 meters long. Find the perimeter of the rhombus.
One of the internal angles of the rhombus is 120°, and the shorter diagonal is 3.4 meters long. Find the perimeter of the rhombus.
