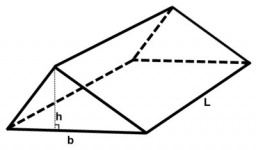
Triangular prism
Calculate the volume of a triangular prism 10 cm high, the base of which is an equilateral triangle with dimensions a = 5 cm and height va = 4,3 cm
Correct answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
Calculation of an equilateral triangle.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Triangular 6345
 Calculate the volume and surface of a triangular prism whose base is a right triangle with sides a = 3m, b = Va = 4m, and c = 5m. The height of the prism is v = 5.5 m.
Calculate the volume and surface of a triangular prism whose base is a right triangle with sides a = 3m, b = Va = 4m, and c = 5m. The height of the prism is v = 5.5 m. - Triangular prism
 Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm. ..Va = 4 dm. (base edge length and base triangle height length) ... ... .v = 23 dm (body height)
Calculate the volume and surface area of a triangular prism if it is given: a = 6.8 dm. ..Va = 4 dm. (base edge length and base triangle height length) ... ... .v = 23 dm (body height) - Perpendicular 6624
 A = 3 cm b = 4 cm prism height h = 10cm Calculate the volume of a triangular prism with the base of a right triangle - the perpendicular a, b.
A = 3 cm b = 4 cm prism height h = 10cm Calculate the volume of a triangular prism with the base of a right triangle - the perpendicular a, b. - Triangular prism - regular
 The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism.
The regular triangular prism is 7 cm high. Its base is an equilateral triangle whose height is 3 cm. Calculate the surface and volume of this prism. - Trapezoidal prism
 Calculate the volume of a prism with a trapezoidal base with side a = 6 dm, side c = 4 dm, and height of the prism = 8dm. The height of the trapezoid is va = 3dm.
Calculate the volume of a prism with a trapezoidal base with side a = 6 dm, side c = 4 dm, and height of the prism = 8dm. The height of the trapezoid is va = 3dm. - Triangular prism
 Calculate the surface area and volume of a three-sided prism with a base of a right-angled triangle, if its sides are a=3cm, b=4cm, c=5cm and the height of the prism is v=12cm.
Calculate the surface area and volume of a three-sided prism with a base of a right-angled triangle, if its sides are a=3cm, b=4cm, c=5cm and the height of the prism is v=12cm. - Hexagonal prism
 The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism.
The prism's base is a regular hexagon consisting of six triangles with side a = 12 cm and height va = 10.4 cm. The prism height is 5 cm. Find the volume and surface of the prism. - Triangular prism
 Calculate the volume and surface of the triangular prism ABCDEF with the base of an isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm.
Calculate the volume and surface of the triangular prism ABCDEF with the base of an isosceles triangle. Base's height is 16 cm, leg 10 cm, base height vc = 6 cm. The prism height is 9 cm. - Triangular prism
 Calculate the surface of a triangular prism 10 cm high, the base of which is a triangle with sides of 6 cm, 8 cm, and 8 cm
Calculate the surface of a triangular prism 10 cm high, the base of which is a triangle with sides of 6 cm, 8 cm, and 8 cm - Perpendicular 3482
 The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle.
The lengths of the base legs are 7.2 cm and 4.7 cm, and the height of the prism is 24 cm. Calculate the volume and surface of a triangular perpendicular prism with the base of a right triangle. - Triangular prism
 Calculate the surface of a triangular prism with the base of an equilateral triangle with a side length of 7.5 cm and a corresponding height of 6.5 cm. Prism height is 15cm.
Calculate the surface of a triangular prism with the base of an equilateral triangle with a side length of 7.5 cm and a corresponding height of 6.5 cm. Prism height is 15cm. - Triangular pyramid
 Calculate the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height v = 20cm.
Calculate the volume of a regular triangular pyramid with edge length a = 12cm and pyramid height v = 20cm. - Prism - eq triangle
 Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm.
Calculate the volume and surface of the prism with the base of an equilateral triangle with side a = 4cm, and the body height is 6cm. - Equilateral 2714
 Determine the volume and surface of a 9 cm high triangular prism if the base is an equilateral triangle with a side of 8 cm.
Determine the volume and surface of a 9 cm high triangular prism if the base is an equilateral triangle with a side of 8 cm. - Perpendicular 35183
 Calculate the surface and volume of a vertical prism if its height h = 18 cm and if the base is an equilateral triangle with side length a = 7.5 cm.
Calculate the surface and volume of a vertical prism if its height h = 18 cm and if the base is an equilateral triangle with side length a = 7.5 cm. - Triangular prism
 Calculate a triangular prism if it has a rectangular triangle base with a = 4cm and hypotenuse c = 50mm, and the height of the prism is 0.12 dm.
Calculate a triangular prism if it has a rectangular triangle base with a = 4cm and hypotenuse c = 50mm, and the height of the prism is 0.12 dm. - Right triangular prism
 We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area
We have a cuboid with a base and dimensions of 12 cm and 5 cm and a height of 4 cm. The tablecloth is cut into two identical triangular prisms with right triangular bases. We painted the surface of the created prisms with color. Calculate the surface area
