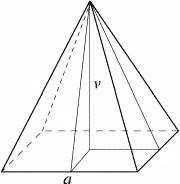
4s pyramid
A regular tetrahedral pyramid has a base edge a=17 and a collateral edge length b=32.
What is its height?
What is its height?
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Circumference of edges
 The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume.
The hexagon pyramid has a circumference of 120 cm, and the length of the side edge is 25 cm. Calculate its volume. - Slant height 2
 A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid.
A regular triangular pyramid with a slant height of 9 m has a volume of 50 m³. Find the lateral area of the pyramid. - School model
 The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³
The beech school model of a regular quadrilateral pyramid has a base 20 cm long and 24 cm high. Calculate a) the surface of the pyramid in square decimeters, b) the mass of the pyramid in kilograms if the density of the beech is ρ = 0,8 g/cm³ - How to
 How to find a total surface of a rectangular pyramid if each face is 8 dm high and the base is 10 dm by 6 dm?
How to find a total surface of a rectangular pyramid if each face is 8 dm high and the base is 10 dm by 6 dm?
- Regular quadrilateral pyramid
 Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge a applies: V = 2.8 m³, v = 2.1 m
Find the surface area of a regular quadrilateral pyramid if for its volume V and body height v and the base edge a applies: V = 2.8 m³, v = 2.1 m - Triangular 46641
 The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume. - The roof
 The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed?
The house's roof has the shape of a regular quadrilateral pyramid 5 m high and the edge of the base 7 m. How many tiles with an area of 540 cm² are needed? - The roof
 The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste.
The tower's roof has the shape of a regular quadrangular pyramid, the base edge of which is 11 m long, and the side wall of the animal with the base at an angle of 57°. Calculate how much roofing we need to cover the entire roof if we count on 15% waste. - Base diagonal
 In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.
In a regular 4-sided pyramid, the side edge forms an angle of 55° with the base's diagonal. The length of the side edge is eight meters. Calculate the surface area and volume of the pyramid.
- Side edges
 The regular 4-sided pyramid has a body height of 2 dm, and the opposite side edges form an angle of 70°. Calculate the surface area and volume of the pyramid.
The regular 4-sided pyramid has a body height of 2 dm, and the opposite side edges form an angle of 70°. Calculate the surface area and volume of the pyramid. - Truncated pyramid
 Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm.
Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, and height v = 8 cm. - Truncated pyramid
 Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees.
Find the volume of a regular 4-sided truncated pyramid if a1 = 14 cm, a2 = 8 cm, and the angle that the side wall with the base is 42 degrees. - Pentagonal pyramid
 The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid.
The height of a regular pentagonal pyramid is as long as the edge of the base, 20 cm. Calculate the volume and surface area of the pyramid. - Regular 4-sided pyramid
 Find the area (surface area) of a regular 4-sided pyramid if its height is 20 m and the wall height is 23 m.
Find the area (surface area) of a regular 4-sided pyramid if its height is 20 m and the wall height is 23 m.
- Quadrilateral pyramid
 Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8cm and a wall height w = 10cm. Sketch a picture.
Find the height and surface of a regular quadrilateral pyramid with a base edge a = 8cm and a wall height w = 10cm. Sketch a picture. - The pyramid
 The pyramid with a square base is 50 m high, and the sidewall height is 80 m. Find the edge of the base of the pyramid.
The pyramid with a square base is 50 m high, and the sidewall height is 80 m. Find the edge of the base of the pyramid. - Pentagonal pyramid
 Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
Find the volume and surface of a regular pentagonal pyramid with a base edge a = 12.8 cm and a height v = 32.1 cm.
