MO Z8-I-1 2018
Fero and David meet daily in the elevator. One morning, they found that if they multiply their current age, they get 238. If they did the same after four years, this product would be 378. Determine the sum of the current ages of Fero and David.
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Do you want to convert time units like minutes to seconds?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- integer equation
- system of equations
- biquadratic equation
- basic functions
- reason
- numbers
- natural numbers
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Vertex of the rectangle
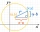 Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0
Determine the coordinates of the vertex of the rectangle inscribed in the circle x²+y² -2x-4y-20=0 if you know that one of its sides lies on the line p: x+2y=0 - General right triangle
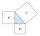 In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse.
In a right triangle, if a =x+34 and b = x and c= 50, then solve for x. Side c is a hypotenuse. Then discuss the case when a or b is a hypotenuse. - Peter 16
 Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed
Peter travels to his uncle's home, 30 km away from his place. He cycles for 2/3 of the journey before the cycle develops a mechanical problem, and he has to push it for the rest of the journey. If he is cycling 10 km per hour faster than his walking speed - The factory 3
 The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl
The factory is 18 km away from the city. A cyclist leaves the factory for the city, and half an hour after him from the same place, a motorcyclist arrives 6 minutes before the cyclist in the city. Find the speed of each, knowing that the speed of the cycl - Mountain climbing
 Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x?
Ken and his brother decided to go on mountain climbing 8 miles from their house to Mt. Daraitan at a rate of x mph (miles per hour). For the return trip, it was 2 mph faster. It took them 6 hours for the entire round trip. What is the x? - A speedboat
 A speedboat goes 900 km against a current of 25 km/hr. Its trip took 10 minutes longer than it would have taken to travel with the current. What is the speedboat's speed in still water?
A speedboat goes 900 km against a current of 25 km/hr. Its trip took 10 minutes longer than it would have taken to travel with the current. What is the speedboat's speed in still water? - A boy 2
 A boy dropped a coin from the top of the dry well and heard a sound 6 seconds later. Considering this as a free-fall object, how deep is the well? The speed of sound in air is approximately 343 m/s.
A boy dropped a coin from the top of the dry well and heard a sound 6 seconds later. Considering this as a free-fall object, how deep is the well? The speed of sound in air is approximately 343 m/s. - Vertically 65984
 We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m?
We threw the stone vertically upwards at a speed of v = 15m. s-1. How long will it be at a) 10 m, b) 12 m? - Magnitudes 64704
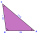 The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '.
The triangle ABC determines the size of the sides a and b and the magnitudes of the interior angles β and γ, given c = 1.86 m, the line on the side c is 2.12 m, and the angle alpha is 40 ° 12 '. - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - At what
 At what speed did the motorist drive when he reacted by noticing the obstacle by 0.8 s; the magnitude of the opposite acceleration during braking was 6.5 m/s², and the car ran to a stopped track 35 m?
At what speed did the motorist drive when he reacted by noticing the obstacle by 0.8 s; the magnitude of the opposite acceleration during braking was 6.5 m/s², and the car ran to a stopped track 35 m? - A missile
 A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - Two workers
 One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself?
One worker makes a part 4 hours and the second 9 hours later than they would make the same part together. How long does it take for each worker to make the part himself? - The car
 The car weight 1280 kg and increased its speed from 7.3 m/s to 63 km/h on a track of 37.2 m. What force did the car engine have to exert?
The car weight 1280 kg and increased its speed from 7.3 m/s to 63 km/h on a track of 37.2 m. What force did the car engine have to exert? - Height and base
 An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base?
An isosceles triangle has an area of 168 cm², and its added height and base are 370 cm. What are the measurements of its height and base? - The tourist
 The tourist wanted to walk the route 16 km at a specific time. He, therefore, came out at the necessary constant speed. However, after a 4 km walk, he fell unplanned into the lake, where he almost drowned. It took him 20 minutes to get to the shore and re
The tourist wanted to walk the route 16 km at a specific time. He, therefore, came out at the necessary constant speed. However, after a 4 km walk, he fell unplanned into the lake, where he almost drowned. It took him 20 minutes to get to the shore and re - Working alone
 Tom and Chandri are doing household chores. Chandri can do the work twice as fast as Tom. If they work together, they can finish the work in 5 hours. How long does it take Tom to work alone to do the same work?
Tom and Chandri are doing household chores. Chandri can do the work twice as fast as Tom. If they work together, they can finish the work in 5 hours. How long does it take Tom to work alone to do the same work?
