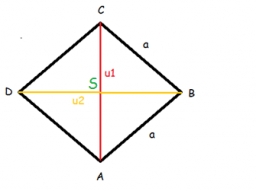
Diagonals of the rhombus
How long are the diagonals e, and f in the diamond if its side is 5 cm long and its area is 20 cm2?
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Trigonometric fx
 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - A right
 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
- Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Acceleration 79164
 A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope?
A skier goes down a slope 66 m long in a uniformly accelerated motion in 10 seconds. With what acceleration was it moving, and what is the slope of the slope? - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - A flagpole
 A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string?
A flagpole is leaning at an angle of 107° with the ground. A string fastened to the top of the flagpole is holding up the pole. The string makes an angle of 38° with the ground, and the flagpole is 8 m long. What is the length of the string? - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
- An angle of depression
 The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse?
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse? - Common chord
 The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two
The common chord of the two circles, c1 and c2, is 3.8 cm long. This chord forms an angle of 47° with the radius r1 in the circle c1. An angle of 24° 30' with the radius r2 is formed in the circle c2. Calculate both radii and the distance between the two - Cosine
 Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? °
Cosine and sine theorem: Calculate all missing values (sides and angles) of the triangle ABC. a = 20 cm; b = 15 cm; γ = 90°; c =? cm; α =? °; β =? ° - Regular octagon pad
 You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - In the 18
 In the right triangle ABC, The hypotenuse AB = 15 cm, and B = 25 degree. How long is BC to the nearest centimeter?
In the right triangle ABC, The hypotenuse AB = 15 cm, and B = 25 degree. How long is BC to the nearest centimeter?
- A missile
 A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second.
A missile is fired with a speed of 100 fps in a direction 30° above the horizontal. Determine the maximum height to which it rises. Fps foot per second. - Centre of the hypotenuse
 The interior angles of the triangle ABC, alpha, beta, and gamma are in a ratio of 1:2:3. The longest side of the AB triangle is 30 cm long. Calculate the perimeter of the triangle CBS if S is the center of the side AB.
The interior angles of the triangle ABC, alpha, beta, and gamma are in a ratio of 1:2:3. The longest side of the AB triangle is 30 cm long. Calculate the perimeter of the triangle CBS if S is the center of the side AB. - Parallelogram diagonals
 Find the area of a parallelogram if the diagonals u1 = 15 cm, u2 = 12 cm, and the angle formed by them is 30 degrees.
Find the area of a parallelogram if the diagonals u1 = 15 cm, u2 = 12 cm, and the angle formed by them is 30 degrees.
