Road
Between cities A and B is a route 13 km long of average 7‰ stúpanie. Calculate the height difference between cities A and B.
Correct answer:

Tips for related online calculators
Our permille calculator will help you quickly calculate various typical tasks with permilles.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- planimetrics
- right triangle
- triangle
- basic functions
- per mil
- goniometry and trigonometry
- sine
- tangent
- arctangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Mast angles and height
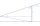 Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast.
Calculate the height of the mast, whose foot can be seen at a depth angle of 11° and the top at a height angle of 28°. The mast is observed from a position 10 m above the level of the base of the mast. - A lighthouse
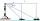 A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats?
A lighthouse overlooks a bay, and it is 77 meters high. From the top, the lighthouse keeper can see a yacht southward at an angle of depression of 32 degrees and another boat eastward at an angle of 25 degrees. What is the distance between the boats? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - A boy 5
 A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A.
A boy starts at A and walks 3km east to B. He then walks 4km north to C. Find the bearing of C from A. - A radio antenna
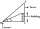 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - A right
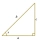 A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x.
A right triangle has side lengths a=3, b=5, and c=4, as shown below. Use these lengths to find tan x, sin x, and cos x. - In the desert
 A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point?
A man wondering in the desert walks 5.7 miles in the direction S 26° W. He then turns 90° and walks 9 miles in the direction N 49° W. At that time, how far is he from his starting point, and what is his bearing from his starting point? - Crosswind
 A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed?
A plane is traveling 45 degrees N of E at 320 km/h when it comes across a current from S of E at 115 degrees of 20 km/h. What are the airplane's new course and speed? - Big tree
 You are standing 20 feet away from a tree, and you measure the angle of elevation to be 38°. How tall is the tree?
You are standing 20 feet away from a tree, and you measure the angle of elevation to be 38°. How tall is the tree? - Sin cos tan
 If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y)
If cos y = 0.8, 0° ≤ y ≤ 90°, find the value of (4 tan y) / (cos y-sin y) - ABS, ARG, CONJ, RECIPROCAL
 Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand
Let z=-√2-√2i where i2 = -1. Find |z|, arg(z), z* (where * indicates the complex conjugate), and (1/z). Where appropriate, write your answers in the form a + i b, where both a and b are real numbers. Indicate the positions of z, z*, and (1/z) on an Argand - A construction
 A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find
A construction worker is trying to find the height of a skyrise building. He is standing some distance away from the base with an angle of elevation of 65 degrees. The worker moves 50 feet closer and measures the angle of elevation to be 75 degrees. Find - Maggie
 Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree.
Maggie observes a car and a tree from a window. The angle of depression of the car is 45 degrees, and that of the tree is 30 degrees. If the distance between the vehicle and the tree is 100 m, find Maggie's distance from the tree. - A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - The airplane
 The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport?
The airplane sights a runway at an angle of depression of 23°. It is flying at an altitude of 3 kilometers above the ground. What is the horizontal distance of the airplane from the airport? - Big tower
 From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place?
From the tower, which is 15 m high and 30 m from the river, the river's width appeared at an angle of 15°. How wide is the river in this place? - The ladder
 The ladder makes an angle of 2°30' with the wall and reaches a height of 2.3 m. How far is the ladder from the wall?
The ladder makes an angle of 2°30' with the wall and reaches a height of 2.3 m. How far is the ladder from the wall?
