Hexagon
Draw a regular hexagon inscribed in a circle with a radius r=8 cm. What is its perimeter?
Correct answer:

Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 82616
 Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD.
Triangle ABC is divided into line segments. Lines DE and AB are parallel. Triangles CDH, CHI, CIE, and FIH have the same area, namely 8 dm². Find the content of quadrilateral AFHD. - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - One side 4
 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
- Regular polygons
 Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x?
Two regular polygons, x and y, are such that the number of sides of x is three more than the number of the sides of y. If the sum of the exterior angles of x and y is 117°, how many sides have x? - Pentagon
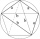 The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm
The signboard has the shape of a pentagon ABCDE, in which line BC is perpendicular to line AB, and EA is perpendicular to line AB. Point P is the heel of the vertical starting from point D on line AB. | AP | = | PB |, | BC | = | EA | = 6dm, | PD | = 8.4dm - Regular octagon pad
 You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci
You need to make a pad in the shape of a regular octagon with a side length of 4 cm. What is the minimum diameter of the circle-shaped semi-finished product from which we make the pad, and what will be the percentage of waste? (Round the results to 1 deci - Goat
 The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent
The fenced flower bed has the shape of a regular hexagon. The tops are formed by fence posts. The fence around the flowerbed measures 60 m. A goat is tied to one of the pillars from the outside and grazes on the surrounding meadow (the goat should not ent - Irregular hexagon
 There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area?
There is an irregular hexagon whose sides are the same length. The opposite sides are parallel; their distance is 237, 195, and193. What is its area?
- Carousel for children
 There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m?
There are 5 seats evenly distributed on the children's carousel in the shape of a circle. What kind the arm of the carousel (connecting the center of the carousel to the seat) is long if the distance between with two seats is 1.2m? - Seats on carousel
 There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m?
There are 12 seats evenly distributed on the children's carousel in the shape of a circle. How long is the arm of the carousel (connecting the center of the carousel to the seat) if the distance between the two seats is 1.5m? - Hexaprism container
 Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm.
Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm. - Hexagonal prism
 Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm.
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - A dodecagon
 Find the surface area of a regular 12-sided polygon if its side is a = 12 cm.
Find the surface area of a regular 12-sided polygon if its side is a = 12 cm.
- Inscribed and described circle
 Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm.
Find the radii of a circle inscribed and circumscribed by a regular pentagon whose side measures 3 cm. - Hexagonal pyramid
 Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m.
Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m. - Quadrilateral 27693
 Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
Construct a quadrilateral ABCD with diagonals AC = e = 7cm, BD = f = 6.2cm, d = 4.3cm, a = 5.3cm and β = 125°
