Investment 2
Jack invested $5000 in a 5-month term deposit at 4.7% pa. At the end of the five months, Jack reinvested the maturity value from the first deposit into an 11-month term deposit at 7.3% pa. What is the maturity value at the end of the second term deposit?
Correct answer:

Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to convert time units like minutes to seconds?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
- algebra
- exponential equation
- geometric progression
- arithmetic
- exponentiation
- basic functions
- percentages
- exponential function
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Flower series
 Every day, the flower develops two new flowers, and each of these new blossoms also bears two flowers each day. After eight days, how many blooms are already present in the garden?
Every day, the flower develops two new flowers, and each of these new blossoms also bears two flowers each day. After eight days, how many blooms are already present in the garden? - Geometric series
 How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity?
How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity? - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Annual interest
 A loan of 10 000 euros is to be repaid in annual payments over ten years. Assuming a fixed 10% annual interest rate compounded annually, calculate: (a) the amount of each annual repayment (b) the total interest paid.
A loan of 10 000 euros is to be repaid in annual payments over ten years. Assuming a fixed 10% annual interest rate compounded annually, calculate: (a) the amount of each annual repayment (b) the total interest paid. - Present value
 A bank loans a family $90,000 at a 4.5% annual interest rate to purchase a house. The family agrees to pay the loan off by making monthly payments over 15 years. How much should the monthly payment be in order to pay off the debt in 15 years?
A bank loans a family $90,000 at a 4.5% annual interest rate to purchase a house. The family agrees to pay the loan off by making monthly payments over 15 years. How much should the monthly payment be in order to pay off the debt in 15 years? - Savings
 Suppose on your 21st birthday you begin making monthly payments of $500 into an account that pays 8% compounded monthly. If you continue the payments until your 51st birthday (30 years), How much money is in your account? How much of it is interesting? Sh
Suppose on your 21st birthday you begin making monthly payments of $500 into an account that pays 8% compounded monthly. If you continue the payments until your 51st birthday (30 years), How much money is in your account? How much of it is interesting? Sh - Sum of GP members
 Determine the sum of the GP 30, 6, 1.2, to 5 terms. What is the sum of all terms (to infinity)?
Determine the sum of the GP 30, 6, 1.2, to 5 terms. What is the sum of all terms (to infinity)? - Fly and cyclist
 Two cyclists are 20 km apart on the same line. They start at the same time as each other at a speed of 10 km/hr. A fly sitting on one of the cyclist's handles starts flying toward the other cyclists at a speed of 20 km/hr. It touches the handle and moves
Two cyclists are 20 km apart on the same line. They start at the same time as each other at a speed of 10 km/hr. A fly sitting on one of the cyclist's handles starts flying toward the other cyclists at a speed of 20 km/hr. It touches the handle and moves - Exponential decay
 A tank contains 55 liters of water. Water is flowing out at the rate of 7% per minute. How long does it take to drain the tank?
A tank contains 55 liters of water. Water is flowing out at the rate of 7% per minute. How long does it take to drain the tank? - Pilsen circus
 A city citizen saw the circus's arrival in Pilsen in the morning at 08:00. He passed this information at 08:15 to three other city residents. Each of these three people then informed the other three residents at 08:30, and again at 08:45, they reported th
A city citizen saw the circus's arrival in Pilsen in the morning at 08:00. He passed this information at 08:15 to three other city residents. Each of these three people then informed the other three residents at 08:30, and again at 08:45, they reported th - Infinite sum of areas
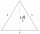 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Population growth
 How many people will be on Earth from two people for 5,000 years if every couple always has four children (2 boys and two girls) at the age of 25-35, and every man will live 75 years?
How many people will be on Earth from two people for 5,000 years if every couple always has four children (2 boys and two girls) at the age of 25-35, and every man will live 75 years? - Infinite decimal
 Imagine the infinite decimal number 0.99999999... That is a decimal and her endless series of nines. Determine how much this number is less than the number 1. Thank you in advance.
Imagine the infinite decimal number 0.99999999... That is a decimal and her endless series of nines. Determine how much this number is less than the number 1. Thank you in advance. - Series and sequences
 Find a fraction equivalent to the recurring decimal. 0.435643564356
Find a fraction equivalent to the recurring decimal. 0.435643564356 - To the cinema
 Jane at 8 AM got a message that all 1093 school pupils would go to the cinema. Within 20 min she said it to the three friends. Each of them again for 20 minutes said to the other three. In this way, the message spread further. At what time do all the scho
Jane at 8 AM got a message that all 1093 school pupils would go to the cinema. Within 20 min she said it to the three friends. Each of them again for 20 minutes said to the other three. In this way, the message spread further. At what time do all the scho - Miraculous tree
 The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days?
The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days? - Hot air balloon
 A hot air balloon ascends 25 meters up for a minute after launch. Every minute ascends 75 percent of the height, which climbed in the previous minute. a) how many meters ascend six minutes after takeoff? b) what is the overall height 10 minutes after laun
A hot air balloon ascends 25 meters up for a minute after launch. Every minute ascends 75 percent of the height, which climbed in the previous minute. a) how many meters ascend six minutes after takeoff? b) what is the overall height 10 minutes after laun
