Touch x-axis
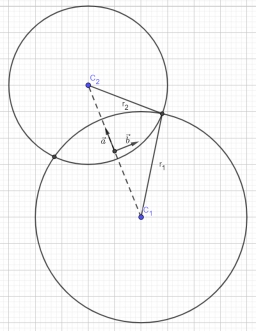
Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Lara's sequence
 Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with?
Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with? - Empty rooms
 In the tourist dormitory, 44 students slept in eight rooms, some of which were four-bed and others six-bed. When two beds were empty, how many four-bed and six-bed rooms were there in the dormitory?
In the tourist dormitory, 44 students slept in eight rooms, some of which were four-bed and others six-bed. When two beds were empty, how many four-bed and six-bed rooms were there in the dormitory? - One muffin
 Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin.
Eight muffins and one drink cost $8.12. If the drink costs $1.24, find the cost of one muffin. - Gasoline 15
 A car consumes 8 liters of gasoline for 20km. How far can it go for 36 liters?
A car consumes 8 liters of gasoline for 20km. How far can it go for 36 liters?
- 13 times
 1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box.
1/3 times the sum of a number, and 2.6 is 4.9. What is the number? Enter your answer as a simplified mixed number in the box. - The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - Fraction money
 5/8 of a sum of money is £1.10. What is the whole amount?
5/8 of a sum of money is £1.10. What is the whole amount? - Fraction equation 3
 A number minus one-ninth equals one-half. Find the number.
A number minus one-ninth equals one-half. Find the number. - Farmer 8
 Farmer George cultivated 7/12 of his land with oranges and 1/5 of the remainder with cherries, and the remaining 40 acres he planted with cash crops. How much land did the farmer cultivate in all? What fraction of land does she plant with cherries?
Farmer George cultivated 7/12 of his land with oranges and 1/5 of the remainder with cherries, and the remaining 40 acres he planted with cash crops. How much land did the farmer cultivate in all? What fraction of land does she plant with cherries?
- The difference 6
 The difference between a number and 15 is multiplied by -3, and the result is - 30
The difference between a number and 15 is multiplied by -3, and the result is - 30 - Dimensions 83176
 If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions
If we reduce the length of the rectangle by 2 cm and the width by 1 cm, its area will decrease by 8 cm². If we increase the length of the rectangle by 1 cm and the width by 2 cm, then its content will increase by 13 cm². What were the original dimensions - A right 3
 A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides .
A right triangle has a perimeter of 300 cm . its hypotenuse is 130cm. What are the lengths of the other sides . - The enrolment 2
 The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment?
The enrolment at a school has increased from 1400 learners to 1600 learners over 5 years. What is the percentage increase in enrolment? - Fraction number
 If two-thirds of a number is added to one-ninth of the same number, the result is 7. Find the number.
If two-thirds of a number is added to one-ninth of the same number, the result is 7. Find the number.
- Circumferences 83111
 Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape.
Péta composed several planar shapes from mutually congruent triangles. The circumferences of the first three are 8 cm, 11.4 cm, and 14.7 cm, respectively. Determine the perimeter of the fourth shape. - Gift baskets
 Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas
Alessia and Alexia made some gift baskets to sell. 2/5 of them were Yu-Gi-oh themed, and the rest were Barbie-themed. They sold 3/4 of the yu-gi-oh-themed baskets and 7/12 of the Barbie-themed baskets. They remained with 56 gift baskets. How many gift bas - Cupcakes
 Keia and Hiro made a total of 27 cupcakes. Keia made 2 times as many cupcakes as Hiro. How many cupcakes did Hiro make?
Keia and Hiro made a total of 27 cupcakes. Keia made 2 times as many cupcakes as Hiro. How many cupcakes did Hiro make?
