Touch x-axis
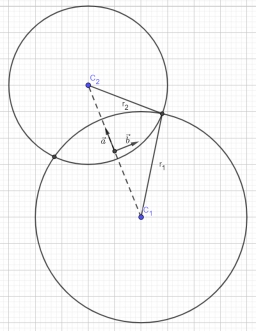
Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Quadrilateral 2
 Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles.
Show that the quadrilateral with vertices P1(0,1), P2(4,2), P3(3,6) P4(-5,4) has two right triangles. - Ratio of sides
 Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7. - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Quarter circle
 What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm?
What is the radius of a circle inscribed in the quarter circle with a radius of 100 cm? - Cylinder horizontally
 The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder?
The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the cylinder's axis. How many hectoliters of water is in the cylinder? - Parallelogram 5027
 Calculate the area of the parallelogram if the side sizes are a = 80, b = 60, and the size of the diagonal angle is 60°.
Calculate the area of the parallelogram if the side sizes are a = 80, b = 60, and the size of the diagonal angle is 60°. - Circular segment
 Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ)
Calculate the area S of the circular segment and the length of the circular arc l. The height of the circular segment is 2 cm, and the angle α = 60°. Help formula: S = 1/2 r². (Β-sinβ) - Circular ring
 A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form.
A square with an area of 16 centimeters is inscribed circle k1 and described to circle k2. Calculate the area of the circular ring, which circles k1, and k2 form. - Circular pool
 The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool?
The pool's base is a circle with a radius r = 10 m, excluding a circular segment that determines the chord length of 10 meters. The pool depth is h = 2m. How many hectoliters of water can fit into the pool? - Calculate triangle
 In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm.
In the triangle, ABC, calculate the sizes of all heights, angles, perimeters, and area if given a=40cm, b=57cm, and c=59cm. - Angle of diagonals
 Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°.
Calculate a rectangle's perimeter and area if its diagonal is 14 cm and the diagonals form an angle of 130°. - Maximum of volume
 The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum?
The shell of the cone is formed by winding a circular section with a radius of 1. For what central angle of a given circular section will the volume of the resulting cone be maximum? - Quadrilateral pyramid
 The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place.
The height of a regular quadrilateral pyramid is 6.5 cm, and the angle between the base and the side wall is 42°. Calculate the surface area and volume of the body—round calculations to 1 decimal place. - Quadrilateral oblique prism
 What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°?
What is the volume of a quadrilateral oblique prism with base edges of length a = 1m, b = 1.1m, c = 1.2m, d = 0.7m if a side edge of length h = 3.9m has a deviation from the base of 20° 35' and the edges a, b form an angle of 50.5°? - Flakes
 A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips?
A circle was inscribed in the square. We draw a semicircle above each side of the square as above the diameter. This resulted in four chips. Which is bigger: the area of the middle square or the area of the four chips? - The trapezium
 The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium.
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium. - Company logo
 The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
The company logo consists of a blue circle with a radius of 4 cm and an inscribed white square. What is the area of the blue part of the logo?
