Angles in a triangle
The angles of the triangle ABC make an arithmetic sequence with the largest angle γ=83°.
What sizes have other angles in a triangle?
What sizes have other angles in a triangle?
Correct answer:
Tips for related online calculators
Looking for help with calculating arithmetic mean?
Looking for a statistical calculator?
Do you have a system of equations and looking for calculator system of linear equations?
See also our trigonometric triangle calculator.
Looking for a statistical calculator?
Do you have a system of equations and looking for calculator system of linear equations?
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - Angles in a triangle
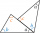 In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle?
In a triangle, the first angle measures a number plus 45°, and the second angle is 30° less than the first angle. The third angle is two times the number more than the first angle. What are the measurements of each angle of the triangle? - One angle
 One angle is 10 degrees more than four times the measure of the other angle. Together they have a sum of 120 degrees. What is the measure of each angle?
One angle is 10 degrees more than four times the measure of the other angle. Together they have a sum of 120 degrees. What is the measure of each angle? - Temperature linear fit
 At 2:00 a.m., the temperature was -7°F. At noon the temperature was 18°F. What expression represents the increase in temperature?
At 2:00 a.m., the temperature was -7°F. At noon the temperature was 18°F. What expression represents the increase in temperature?
- Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Vector v4
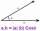 Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - The tower
 The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands?
The observer sees the tower's base 96 meters high at a depth of 30 degrees and 10 minutes and the top of the tower at a depth of 20 degrees and 50 minutes. How high is the observer above the horizontal plane on which the tower stands? - One-quarter 13953
 Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma.
Calculate the magnitude of the interior angles of the triangle ABC if alpha = two-fifths beta and alpha = one-quarter gamma. - Three parallels
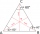 The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
The vertices of an equilateral triangle lie on three different parallel lines. The middle line is 5 m and 3 m distant from the end lines. Calculate the height of this triangle.
- Calculate 9701
 In the triangle, the side length AB = 6 cm, the height per side c = 5 cm, and the angle BCA = 35°. Calculate sides a b.
In the triangle, the side length AB = 6 cm, the height per side c = 5 cm, and the angle BCA = 35°. Calculate sides a b. - The second
 The second angle of a triangle is the same size as the first angle. The third angle is 12 degrees larger than the first angle. How large are the angles?
The second angle of a triangle is the same size as the first angle. The third angle is 12 degrees larger than the first angle. How large are the angles? - Triangle 42
 Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=?
Triangle BCA. Angles A=119° B=(3y+14) C=4y. What is the measure of triangle BCA=? - Angle at the apex
 In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles?
In an isosceles triangle, the angle at the apex is 30° greater than the angle at the base. How big are the internal angles? - Supplementary angles
 One of the supplementary angles is larger by 33° than the second one. Calculate the angle size.
One of the supplementary angles is larger by 33° than the second one. Calculate the angle size.
- In a 2
 In a thirteen-sided polygon, the sum of five angles is 1274°, four of the eight angles remaining are equal, and the other four are 18° less than each of the equal angles. Find the angles.
In a thirteen-sided polygon, the sum of five angles is 1274°, four of the eight angles remaining are equal, and the other four are 18° less than each of the equal angles. Find the angles. - Six-sided polygon
 There is a six-sided polygon. The first two angles are equal, the third angle is twice (the equal angles), two other angles are trice the equal angle, while the last angle is a right angle. Find the value of each angle.
There is a six-sided polygon. The first two angles are equal, the third angle is twice (the equal angles), two other angles are trice the equal angle, while the last angle is a right angle. Find the value of each angle. - Right triangle eq2
 Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
Find the lengths of the sides and the angles in the right triangle. Given area S = 210 and perimeter o = 70.
