Stamps
Tibor has four times more stamps than Miro and seven times more stamps than Stano. How many stamps have all three if Tibor has 504 stamps?
Correct answer:

You need to know the following knowledge to solve this word math problem:
Related math problems and questions:
- Triangular 81985
 Trainees stand on the marks in rows exactly 1.5 m apart. They form an expanding triangular wedge (in each subsequent row, there is one more exerciser), while the distance between the front exerciser and the back row is 30 m. Determine the number of traine
Trainees stand on the marks in rows exactly 1.5 m apart. They form an expanding triangular wedge (in each subsequent row, there is one more exerciser), while the distance between the front exerciser and the back row is 30 m. Determine the number of traine - Geometric series
 How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity?
How many terms of the geometric series 8+4+2+1+0.5+... must be taken for the sum to get within 10 to the power minus 4 of its sum to infinity? - Infinite sum of areas
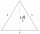 An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the
An equilateral triangle A1B1C1 is constructed above the height of the equilateral triangle ABC is constructed as. Above the height of the equilateral triangle A1B1C1 is built triangle A2B2C2, and so on. The procedure is repeated continuously. What is the - Series and sequences
 Find a fraction equivalent to the recurring decimal. 0.435643564356
Find a fraction equivalent to the recurring decimal. 0.435643564356
- Miraculous tree
 The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days?
The miraculous tree grows so fast that the first day increases its height by half the total height of the second day by the third, the third day by a quarter, etc. How many times will it increase its height after 6 days? - Saving per cents
 The first day I saved 1 cent and every following day a cent more. How many do I save in one year (365 days)?
The first day I saved 1 cent and every following day a cent more. How many do I save in one year (365 days)? - Decimal to fraction
 Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures.
Write the decimal number 8.638333333 as a fraction A/B in the basic form. Given decimal has infinite repeating figures. - Fraction
 Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator.
Fraction frac(0, overline(38))(0,38) write as fraction a/b, a, b is integers numerator/denominator. - Recursion squares
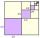
 In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 16 cm. Calculate: a) the sum of peri
In the square, ABCD has inscribed a square so that its vertices lie at the centers of the sides of the square ABCD. The procedure of inscribing the square is repeated this way. The side length of the square ABCD is a = 16 cm. Calculate: a) the sum of peri
- Lara's sequence
 Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with?
Lara starts with a number less than 20. She divides it by 2 adds 6. She then divides this result by 3 her answer is 4.5 What number does she start with? - Sugar 9
 Joe has two containers of sugar. One container has 1 2/5 cups, and the other has 4 1/10 cups. If he uses 1 4/5 of sugar, how much does he have left?
Joe has two containers of sugar. One container has 1 2/5 cups, and the other has 4 1/10 cups. If he uses 1 4/5 of sugar, how much does he have left? - Saravanan
 Saravanan's father bought 2 3/4 m, 2 1/2 m, and 1 1/4 m of cloth. What was the total length of the cloth he bought?
Saravanan's father bought 2 3/4 m, 2 1/2 m, and 1 1/4 m of cloth. What was the total length of the cloth he bought? - Monthly expenses
 John's monthly expenses are analyzed as follows: 1/8 for stationery, 1/3 for fuel, 1/6 for parking, and the rest for food. His total expenses are 4500. Calculate the rand value of the food expenses.
John's monthly expenses are analyzed as follows: 1/8 for stationery, 1/3 for fuel, 1/6 for parking, and the rest for food. His total expenses are 4500. Calculate the rand value of the food expenses. - Water per day
 Liam's goal is to drink 12 cups of water a day. So far, Liam has drank one-half gallon of water today. How much more water, in OUNCES, does Liam need to drink today to reach his goal of 12 cups of water per day?
Liam's goal is to drink 12 cups of water a day. So far, Liam has drank one-half gallon of water today. How much more water, in OUNCES, does Liam need to drink today to reach his goal of 12 cups of water per day?
- Vidya
 Vidya and Peter went for a picnic. Their mother gave them a 5-liter water bottle. Vidya consumed 2/5 of the water, and Peter consumed the remaining water. How much water did Vidya drink? How much water did Peter drink?
Vidya and Peter went for a picnic. Their mother gave them a 5-liter water bottle. Vidya consumed 2/5 of the water, and Peter consumed the remaining water. How much water did Vidya drink? How much water did Peter drink? - Human population
 The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4?
The populations of two cities after t years can be modeled by -150t+50,000 and 50t+75,000. What is the difference in the populations of the towns when t=4? - Megapolis
 The total population of a city consists of 641,682 male adults, 593,118 female adults, and 182,345 children. Find the total population of the city.
The total population of a city consists of 641,682 male adults, 593,118 female adults, and 182,345 children. Find the total population of the city.
