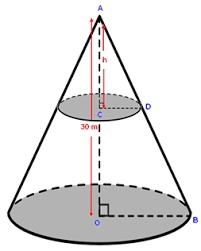
Right circular cone
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone.
Correct answer:
Showing 1 comment:
Dr Math
1:3 is the ratio of heights
1:32 = 1:9 is the ratio of the area of base circles... due to two dimensional nature of the area.
1:33 = 1:27 is the ratio of volumes... .. volume has three-dimensional nature
1:32 = 1:9 is the ratio of the area of base circles... due to two dimensional nature of the area.
1:33 = 1:27 is the ratio of volumes... .. volume has three-dimensional nature
Tips for related online calculators
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- geometry
- similarity of triangles
- arithmetic
- third power
- solid geometry
- similarity bodies
- cone
- planimetrics
- triangle
- basic functions
- ratio
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon. - A teacher 3
 A teacher gives pens and pencils to elementary students at an equal rate, each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the missing value for the letter B.
A teacher gives pens and pencils to elementary students at an equal rate, each classroom. Pencils; Pens 18 ; 72 29 ; A 35 ; 140 B ; 168 Determine the missing value for the letter B. - The proportion
 The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term.
The proportion's first, second, and third terms are 4, 20, and 13. Find the fourth term. - Charter flying service
 Henry and Wayne operate a charter flying service out of Breckenridge, which has an elevation of 9,600 feet above sea level. Henry has two flights scheduled for the day. He is taking a couple from Breckenridge to Hamilton, which has a 35% elevation drop. A
Henry and Wayne operate a charter flying service out of Breckenridge, which has an elevation of 9,600 feet above sea level. Henry has two flights scheduled for the day. He is taking a couple from Breckenridge to Hamilton, which has a 35% elevation drop. A - Sides ratio and angles
 In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC.
In triangle ABC, you know the ratio of side lengths a:b:c=3:4:6. Calculate the angle sizes of triangle ABC. - Julia - recipe
 Julia is using 60 g of butter in a recipe. She needs to use a butter-to-sugar ratio of 6:5. How much sugar should she use?
Julia is using 60 g of butter in a recipe. She needs to use a butter-to-sugar ratio of 6:5. How much sugar should she use? - A cone 4
 A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts. - The ratio 19
 The ratio of males to females in a school is 1:2. If there are 24 pupils, find the number of males.
The ratio of males to females in a school is 1:2. If there are 24 pupils, find the number of males. - Copper 83011
 Brass is an alloy of copper and zinc in a ratio of 3:2. How much copper and zinc do you need to make 1 kilo of brass?
Brass is an alloy of copper and zinc in a ratio of 3:2. How much copper and zinc do you need to make 1 kilo of brass? - Supporting 82880
 Roman and Mathias made a swing in the park by taking a 5 m-long pole and supporting it in the middle. Roman, weighing 52 kg, sat down at the left end. Where should Mathias sit to achieve balance if he weighs 60 kg? Enter the distance measured in meters fr
Roman and Mathias made a swing in the park by taking a 5 m-long pole and supporting it in the middle. Roman, weighing 52 kg, sat down at the left end. Where should Mathias sit to achieve balance if he weighs 60 kg? Enter the distance measured in meters fr - Three in ratio 2
 If 200 is divided into the ratio of 1:2:5, What is the middle quantity?
If 200 is divided into the ratio of 1:2:5, What is the middle quantity? - The sum 43
 The sum of Rs. 820 will be divided among Ali, Fakhar, and Zahid according to the ratio 3 : 4 : 5. How much does each receive?
The sum of Rs. 820 will be divided among Ali, Fakhar, and Zahid according to the ratio 3 : 4 : 5. How much does each receive? - The ratio 18
 The ratio of dogs to cats at a shelter is 2 to 7. If there are 12 dogs, then how many cats are in the shelter?
The ratio of dogs to cats at a shelter is 2 to 7. If there are 12 dogs, then how many cats are in the shelter? - The ratio 17
 The ratio of tomatoes to red apples is 2:5. If there are 20 tomatoes, how many red apples are there?
The ratio of tomatoes to red apples is 2:5. If there are 20 tomatoes, how many red apples are there? - The ratio 16
 Express the following ratio in simplest form: 90:100
Express the following ratio in simplest form: 90:100 - Usain
 Usain and Kyle rented a house together for 3 years. Usain paid more rent because he had a bigger room. They always split the rent at a ratio of 4:3. They paid £30247 in rent over this period. How much of this did Usain pay?
Usain and Kyle rented a house together for 3 years. Usain paid more rent because he had a bigger room. They always split the rent at a ratio of 4:3. They paid £30247 in rent over this period. How much of this did Usain pay?
