Algebra - math word problems - page 77 of 276
Algebra is a branch of mathematics that uses not only numbers and characters but also letters to solve operations. For example 3x+5x is 8x.Number of problems found: 5513
- Tournament 3524
 Four hockey teams scored 337 goals in the tournament. The second team scored 16 goals less than the first, the third 17 less than the second, and the fourth 30 goals less than the second. How many goals did each team score?
Four hockey teams scored 337 goals in the tournament. The second team scored 16 goals less than the first, the third 17 less than the second, and the fourth 30 goals less than the second. How many goals did each team score? - Afternoon 3523
 There were 120 vehicles in the parking lot during the afternoon. CZK 20 for a car and CZK 50 for a bus. The security guard collected a total of 2,640 CZK for parking. How many cars and how many buses were parked in the parking lot
There were 120 vehicles in the parking lot during the afternoon. CZK 20 for a car and CZK 50 for a bus. The security guard collected a total of 2,640 CZK for parking. How many cars and how many buses were parked in the parking lot - Equation
 16 + 2x-7 = 5x + 10-4x
16 + 2x-7 = 5x + 10-4x - Summerjob
 Miloš saved a quarter of the money from the summer job, bought a winter jacket for half, bought gifts for his parents and siblings for a sixth, and still had CZK 400 left. How much did Miloš earn?
Miloš saved a quarter of the money from the summer job, bought a winter jacket for half, bought gifts for his parents and siblings for a sixth, and still had CZK 400 left. How much did Miloš earn? - Identical 3518
 The carpenter cut two identical pieces into shelves from a 2-meter longboard. He cut the rest into four side shelves of 20 cm. How long are the shelves?
The carpenter cut two identical pieces into shelves from a 2-meter longboard. He cut the rest into four side shelves of 20 cm. How long are the shelves? - Interested 3512
 One-third of the 8A class student wants to go to high school after finishing primary school, and half of the students are interested in the field of study. The remaining four have not yet been decided. How many students are there in 8A?
One-third of the 8A class student wants to go to high school after finishing primary school, and half of the students are interested in the field of study. The remaining four have not yet been decided. How many students are there in 8A? - Performance 3510
 They sold 120 tickets at the children's performance for CZK 3,100. The children cost CZK 20, and the adults cost CZK 40. How many children's tickets have been sold?
They sold 120 tickets at the children's performance for CZK 3,100. The children cost CZK 20, and the adults cost CZK 40. How many children's tickets have been sold? - Infinitely 3489
 The solution to the equation 3x = 8x is a / no real number b / x = 8/3 c / x = 3/8 d / x = 0 e / infinitely many solutions
The solution to the equation 3x = 8x is a / no real number b / x = 8/3 c / x = 3/8 d / x = 0 e / infinitely many solutions - Quarter 3421
 Lukáš was saving for new roller skates. The first month he saved a third of their price, the second month a quarter, the third month half of the rest of the price, and the fourth month €25. How much € did the skates cost?
Lukáš was saving for new roller skates. The first month he saved a third of their price, the second month a quarter, the third month half of the rest of the price, and the fourth month €25. How much € did the skates cost? - Roots count
 Substitute the numbers 0,1,2,3 into the equation as x: (x - 1) (x - 3) (x + 1) = 0 Which of them is its solution? Is there another number that solves this equation?
Substitute the numbers 0,1,2,3 into the equation as x: (x - 1) (x - 3) (x + 1) = 0 Which of them is its solution? Is there another number that solves this equation? - Correctness 3416
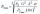 Calculate and verify the correctness of the test result: 12 (3c - 5) + 11 = 10 (8c - 7) - 16c
Calculate and verify the correctness of the test result: 12 (3c - 5) + 11 = 10 (8c - 7) - 16c - Determine 3412
 The average age of the siblings Standy, Radek, and Patricia are ten years. Standa is twice as old as Radek, and Patricia is two years younger than Radek. Determine the age of each sibling.
The average age of the siblings Standy, Radek, and Patricia are ten years. Standa is twice as old as Radek, and Patricia is two years younger than Radek. Determine the age of each sibling. - Three-quarters 3384
 The sum of the two numbers is 75. Find these numbers. Three-quarters of the first are one-seventh of the second.
The sum of the two numbers is 75. Find these numbers. Three-quarters of the first are one-seventh of the second. - Determine 3374
 Pavol, Edita and Juraj have a total of 1243 euros. Pavol has 200 euros more than Edita, Juraj has 457 euros less than Edita. Determine how much each has.
Pavol, Edita and Juraj have a total of 1243 euros. Pavol has 200 euros more than Edita, Juraj has 457 euros less than Edita. Determine how much each has. - Determine 3372
 The son and mother are 32 years old together. My mother is 28 years older. Find how old they are.
The son and mother are 32 years old together. My mother is 28 years older. Find how old they are. - Equation 3364
 Create a number snake from the equation and solve: 2x - 5 = 7 4x + 1/3 = 7 3 (x-2) +4 = 7
Create a number snake from the equation and solve: 2x - 5 = 7 4x + 1/3 = 7 3 (x-2) +4 = 7 - Potatoes bags
 I have three bags with 21 kg of potatoes. The first bag is 5.5 kg more than the second bag, and the third is 0.5 kg more than the second bag. Determine how many kgs of potatoes are in each bag.
I have three bags with 21 kg of potatoes. The first bag is 5.5 kg more than the second bag, and the third is 0.5 kg more than the second bag. Determine how many kgs of potatoes are in each bag. - Machines 3358
 The first machine was made for hours to watch pieces. The more powerful machine produced 32 more watches in the same period. How many watches would both machines produce together in 3 hours?
The first machine was made for hours to watch pieces. The more powerful machine produced 32 more watches in the same period. How many watches would both machines produce together in 3 hours? - Expenditures 3355
 Expenditures on joint trips for pupils were: Travel expenses in euros. Meals in euros. Three nights in euros. Small expenses in euros. Calculate the amount of c that each student paid.
Expenditures on joint trips for pupils were: Travel expenses in euros. Meals in euros. Three nights in euros. Small expenses in euros. Calculate the amount of c that each student paid. - Expression 3350
 Calculate the value of the expression x / y, if you know that (-4x + 3y) / y = 5
Calculate the value of the expression x / y, if you know that (-4x + 3y) / y = 5
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
