Geometry construction - practice problems - page 2 of 10
Number of problems found: 181
- Constructing 67634
 During the construction of a 140-meter-long gas pipeline, a pit with vertical walls 1.5 m deep and 1 m wide must be created. A) How many cubic meters of soil must be dug up? B) We spread the excavated soil evenly on a field with dimensions of 70 m and 120
During the construction of a 140-meter-long gas pipeline, a pit with vertical walls 1.5 m deep and 1 m wide must be created. A) How many cubic meters of soil must be dug up? B) We spread the excavated soil evenly on a field with dimensions of 70 m and 120 - Triangle 67504
 Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 °
Sestroj triangle HOP, if o = 6 cm, h = 8 cm and | PHO | = 90 ° - Symmetrical 67454
 How many more squares in the grid in the picture need to be painted to make it centrally symmetrical? square - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o This is a sketch of a grid where the colored squares are x. Thank you, Lucy
How many more squares in the grid in the picture need to be painted to make it centrally symmetrical? square - x x; o; o; x o; o; x; o x; o; o; o o; x; o; o This is a sketch of a grid where the colored squares are x. Thank you, Lucy - Quadrilateral 67384
 Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees
Construct a quadrilateral ABCD if AB = 10cm, AD = 6cm, DC = 6.5cm and angle BCD = 90 degrees - Coordinates 66474
 Draw a trapezoid in the coordinate system with bases 4cm long, 2cm long, and 3cm high. Please write down the coordinates of its vertices.
Draw a trapezoid in the coordinate system with bases 4cm long, 2cm long, and 3cm high. Please write down the coordinates of its vertices. - Hypotenuse 65744
 Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm
Construct a right triangle ABC with the hypotenuse AB: a) | AB | = 72 mm, | BC | = 51 mm b) | AB | = 58 mm, | AC | = 42 mm - Intersection 64854
 Draw any triangle. Make the axis of its two sides. Their intersection is point S. (a) Measure the distance of point S from all three vertices (b) Draw the axis of the third party.
Draw any triangle. Make the axis of its two sides. Their intersection is point S. (a) Measure the distance of point S from all three vertices (b) Draw the axis of the third party. - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Parallelogram 62084
 OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100 °. What is its area?
OPRS parallelogram with OP side 4 cm long, OS side 5 cm long, angle at the top P is 100 °. What is its area? - (perimeter) 61854
 Construct triangle ABC when we know a + b + c (perimeter), height to side c, and angle gamma.
Construct triangle ABC when we know a + b + c (perimeter), height to side c, and angle gamma. - Trapezoid 61394
 Sestroj trapezoid ABCD, if a = 8cm, b = 5cm, alpha = 60 °, beta = 75 °
Sestroj trapezoid ABCD, if a = 8cm, b = 5cm, alpha = 60 °, beta = 75 ° - Construct 61354
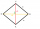 Construct an ABCD diamond with side a = 4.8cm, and the angle at vertex B is 60 °
Construct an ABCD diamond with side a = 4.8cm, and the angle at vertex B is 60 ° - Construct 61253
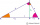 Using Euclid's theorem, construct a line of length √15.
Using Euclid's theorem, construct a line of length √15. - Draw triangle
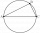 Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37° - Rectangle 60783
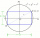 How to build a rectangle using only circles
How to build a rectangle using only circles - Number line
 Visualize and color the following decimal numbers using a grid. 1. 0.35 2. 1.9 3. 0.45 4. 1.15 5. 0.8
Visualize and color the following decimal numbers using a grid. 1. 0.35 2. 1.9 3. 0.45 4. 1.15 5. 0.8 - Square 58873
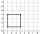 Draw a square so that its sides do not lie on the lines of the square grid
Draw a square so that its sides do not lie on the lines of the square grid - Center-symmetric 58201
 Find out which we can write letters (uppercase) as center-symmetric.
Find out which we can write letters (uppercase) as center-symmetric. - Instructions: 56651
 Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles).
Divide the line segment AB into three equal parts. Instructions: Construct an equilateral triangle ABC and find its center (e.g., the described circles). - Construction 55311
 Construct a KLM triangle where side k is 6.7 cm, the line to the k side is 4.1 cm, and the LKM angle is 63 degrees. Write the construction procedure.
Construct a KLM triangle where side k is 6.7 cm, the line to the k side is 4.1 cm, and the LKM angle is 63 degrees. Write the construction procedure.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
