Geometry - practice problems - page 6 of 153
Number of problems found: 3056
- Geometry: 78014
 Good day, Even though it is a trivial task, I don’t know how to deal with it. This is analytic geometry: Find all integers a, b, and c such that the line given by the equation ax+by=c passes through the points [4,3] and [−2,1]. Thank you for your answer
Good day, Even though it is a trivial task, I don’t know how to deal with it. This is analytic geometry: Find all integers a, b, and c such that the line given by the equation ax+by=c passes through the points [4,3] and [−2,1]. Thank you for your answer - Estimate linear fx
 Which of the following is the best estimate for the temperature at 11 PM if the temperature continues to drop at the same rate? time; temperature °C 3 PM; 32 6 PM; 30 12 PM; 20
Which of the following is the best estimate for the temperature at 11 PM if the temperature continues to drop at the same rate? time; temperature °C 3 PM; 32 6 PM; 30 12 PM; 20 - Calculate 32011
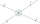 Calculate the size of the BVC angle if the following applies to the size of the angles: AVB = 37 ° 48 minutes, CVD = 52 ° 30 minutes, AVD = 118 °
Calculate the size of the BVC angle if the following applies to the size of the angles: AVB = 37 ° 48 minutes, CVD = 52 ° 30 minutes, AVD = 118 ° - Determine 4649
 Determine five solutions to the equation of two unknowns. Write as arranged pairs and draw in the graph. What does a diagram of a linear equation look like? 2x + 3y = 7
Determine five solutions to the equation of two unknowns. Write as arranged pairs and draw in the graph. What does a diagram of a linear equation look like? 2x + 3y = 7
- Points OPQ
 Point P is on line segment OQ. Given OP = 6, OQ = 4x - 3, and PQ = 3x, find the numerical length of OQ.
Point P is on line segment OQ. Given OP = 6, OQ = 4x - 3, and PQ = 3x, find the numerical length of OQ. - Vector equation
 Let’s v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7) . Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1 c2, c3 and decide weather v, u and w are linear dependent or independent
Let’s v = (1, 2, 1), u = (0, -1, 3) and w = (1, 0, 7) . Solve the vector equation c1 v + c2 u + c3 w = 0 for variables c1 c2, c3 and decide weather v, u and w are linear dependent or independent - Midpoint 5
 FM=3x-4, MG=5x-26, FG=? Point M is the midpoint of FG. Use the given information to find the missing measure or value.
FM=3x-4, MG=5x-26, FG=? Point M is the midpoint of FG. Use the given information to find the missing measure or value. - Line
 Straight-line passing through points A [-3; 22] and B [33; -2]. Determine the total number of points of the line in which both coordinates are positive integers.
Straight-line passing through points A [-3; 22] and B [33; -2]. Determine the total number of points of the line in which both coordinates are positive integers. - Intersection 19343
 What is the sum of all coordinates of points at the intersection of the line p: x = -1-2t, y = 5-4t, z = -3 + 6t, where t is a real number, with the coordinate planes xy and yz?
What is the sum of all coordinates of points at the intersection of the line p: x = -1-2t, y = 5-4t, z = -3 + 6t, where t is a real number, with the coordinate planes xy and yz?
- Perpendicular 82994
 The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis.
The straight line p is given by the formula y = 1/2 x - 1 . The line q is perpendicular to the line p and passes through the point A [1; 5]. Determine the y-coordinate of the point that intersects the line q with the y-axis. - Line
 Write an equation of a line parallel to To 9x + 3y = 8 That Passes Through The Point (-1, -4). Write in the form ax+by=c.
Write an equation of a line parallel to To 9x + 3y = 8 That Passes Through The Point (-1, -4). Write in the form ax+by=c. - Parallel and orthogonal
 I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w
I need math help in this problem: a=(-5, 5 3) b=(-2,-4,-5) (they are vectors) Decompose the vector b into b=v+w where v is parallel to a and w is orthogonal to a, find v and w - Intersection 6374
 Determine the intersection of the two lines p and q if. : p: 3y + 2x-5 = 0 q: 4x + 7y-11 = 0
Determine the intersection of the two lines p and q if. : p: 3y + 2x-5 = 0 q: 4x + 7y-11 = 0 - Three points 4
 The line passed through three points - see table: x y -6 4 -4 3 -2 2 Write line equation in y=mx+b form.
The line passed through three points - see table: x y -6 4 -4 3 -2 2 Write line equation in y=mx+b form.
- Parametric equation
 Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 >
Point A [6; -2]. Point B = [-3; 1] Write the parametric equation of the line BA so that t belongs to the closed interval < 0;3 > - Supplementary angles
 One of the supplementary angles is larger by 33° than the second one. Calculate the angle size.
One of the supplementary angles is larger by 33° than the second one. Calculate the angle size. - Vector v4
 Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1)
Find the vector v4 perpendicular to the vectors v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) and v3 = (0, 0, 1, 1) - Supplementary angles
 One of the supplementary angles is three times larger than the other. What size is larger of supplementary angles?
One of the supplementary angles is three times larger than the other. What size is larger of supplementary angles? - Vector perpendicular
 Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1)
Find the vector a = (2, y, z) so that a⊥ b and a ⊥ c where b = (-1, 4, 2) and c = (3, -3, -1)
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
