Planimetrics - math word problems - page 52 of 169
Study plane measurements, including angles, distances, and areas. In other words - measurement and calculation of shapes in the plane. Perimeter and area of plane shapes.Number of problems found: 3379
- Perpendicular 24671
 The right triangle has an area of 2304 cm2, and one perpendicular is 8 cm long. Express and calculate the second perpendicular.
The right triangle has an area of 2304 cm2, and one perpendicular is 8 cm long. Express and calculate the second perpendicular. - Determine 12331
 An annulus with an area S = 4.2 square meters has an inner radius r = 2.25 m. Determine the outer radius of the annulus.
An annulus with an area S = 4.2 square meters has an inner radius r = 2.25 m. Determine the outer radius of the annulus. - Circumference 10342
 Calculate the area of the rectangle if its circumference is 24cm and one side is 7.2cm long
Calculate the area of the rectangle if its circumference is 24cm and one side is 7.2cm long - Perimeter 9691
 The garden has the shape of a rectangle. The area of the garden is 800.25 square meters. Calculate the garden's perimeter if the length of the garden is 48.5 m.
The garden has the shape of a rectangle. The area of the garden is 800.25 square meters. Calculate the garden's perimeter if the length of the garden is 48.5 m. - Circumference 8771
 Calculate a diamond's area with a circumference of 51.2 cm and a height of 9.6 cm.
Calculate a diamond's area with a circumference of 51.2 cm and a height of 9.6 cm. - Circumference 6338
 The circle has the same area as the square, whose circumference is 400m. Calculate the diameter of the circle.
The circle has the same area as the square, whose circumference is 400m. Calculate the diameter of the circle. - Equilateral 5571
 The height in the equilateral triangle ABC measures the square root of 3 cm. What is the length of the center bar of this triangle?
The height in the equilateral triangle ABC measures the square root of 3 cm. What is the length of the center bar of this triangle? - Calculate 4424
 Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm.
Calculate the area of the triangle ABC if a = 10 cm, c = 8 cm, ta = 6 cm. - Length 4109
 The gym is 16 m wide and has an area of 384 m². Find its length.
The gym is 16 m wide and has an area of 384 m². Find its length. - A yard
 Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length.
Yevgen is fencing in a yard that is 30 meters longer than it is wide. The yard will have an area of 1000 m². Find its width and length. - Length and width
 Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width.
Use the 5-step procedure. The perimeter of a rectangle is 34 in. The length is 4 in less than three times the width. Find the length and width. - Square sides
 If we enlarge the side of the square by a third, its circumference will be 20 cm larger than the original. What is the side of the square?
If we enlarge the side of the square by a third, its circumference will be 20 cm larger than the original. What is the side of the square? - Parallerogram
 The ABCD parallelogram is a = 2.5 cm, height to side a is 7.2 cm, and height to side b is 4 cm. Find the side length b.
The ABCD parallelogram is a = 2.5 cm, height to side a is 7.2 cm, and height to side b is 4 cm. Find the side length b. - Regular n-gon
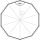 In a regular n-angle polygon, the internal angle is 144 degrees. Find the number n indicating the number of sides of this polygon.
In a regular n-angle polygon, the internal angle is 144 degrees. Find the number n indicating the number of sides of this polygon. - Angles of a triangle
 In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle.
In triangle ABC, the angle beta is 15° greater than the angle alpha. The remaining angle is 30° greater than the sum of the angles alpha and beta. Calculate the angles of a triangle. - Semicircle
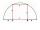 To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides?
To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides? - Arm-leg
 Calculate the length of the base of an isosceles triangle with a circumference 224 cm if the arm length is 68 cm.
Calculate the length of the base of an isosceles triangle with a circumference 224 cm if the arm length is 68 cm. - Rhombus A2p
 The rhombus area is 13 cm², and its height is 5cm long. Find the perimeter of this rhombus.
The rhombus area is 13 cm², and its height is 5cm long. Find the perimeter of this rhombus. - Circle and hexagon
 Calculate the radius of a circle whose circumference is 8.4 cm longer than the inscribed regular hexagon's circumference.
Calculate the radius of a circle whose circumference is 8.4 cm longer than the inscribed regular hexagon's circumference. - Quarter circular
 The wire hooked around the perimeter of the quarter-circular arc has a length of 5π+20. Determine the radius of the circle arc.
The wire hooked around the perimeter of the quarter-circular arc has a length of 5π+20. Determine the radius of the circle arc.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
