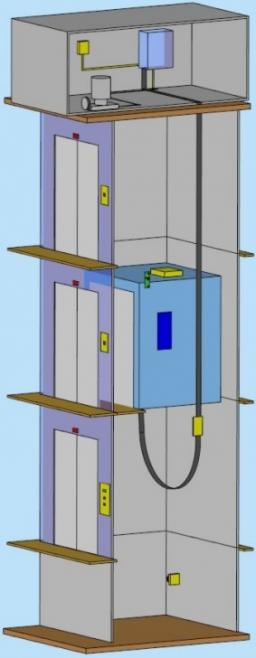
Elevator
In homes with more floors, elevators are used. For passenger transport, the most commonly used traction elevator counterweight. The top of the shaft
engine room with the engine. The car is suspended on a rope, which is guided up over two pulleys to the counterweight.
Consider lift-enabled load Mmax = 300 kg
car weight mk = 500 kg
weight counterweight mz = 650 kg. The cabin moves at the speed
v0 = 1.2 m/s. The total efficiency of power is k =75%.
a) Explain what affects the efficiency of the system and the reason for using a counterweight.
b) Determine the power P1 engine lift if you summon empty cabin residents of the upper floors, which moves down the speed of v0.
c) Determine the power P2 engine lift when a group of citizens with a total mass M = 250 kg conveys speed v0 upwards.
In which of these cases b), c) the need for more power?
g = gravitational constant 10 N/kg
engine room with the engine. The car is suspended on a rope, which is guided up over two pulleys to the counterweight.
Consider lift-enabled load Mmax = 300 kg
car weight mk = 500 kg
weight counterweight mz = 650 kg. The cabin moves at the speed
v0 = 1.2 m/s. The total efficiency of power is k =75%.
a) Explain what affects the efficiency of the system and the reason for using a counterweight.
b) Determine the power P1 engine lift if you summon empty cabin residents of the upper floors, which moves down the speed of v0.
c) Determine the power P2 engine lift when a group of citizens with a total mass M = 250 kg conveys speed v0 upwards.
In which of these cases b), c) the need for more power?
g = gravitational constant 10 N/kg
Correct answer:
Tips for related online calculators
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
Do you want to convert velocity (speed) units?
Do you want to convert time units like minutes to seconds?
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
Related math problems and questions:
- Friction coefficient
 What is the weight of a car when it moves on a horizontal road at a speed of v = 50 km/h at engine power P = 7 kW? The friction coefficient is 0.07
What is the weight of a car when it moves on a horizontal road at a speed of v = 50 km/h at engine power P = 7 kW? The friction coefficient is 0.07 - Power input
 The construction lift lifted a load weighing 300 kg to a height of 12 m with a uniform movement. How long has it taken for the load to be lifted if the efficiency is 75% and the engine has a power input of 5 kW?
The construction lift lifted a load weighing 300 kg to a height of 12 m with a uniform movement. How long has it taken for the load to be lifted if the efficiency is 75% and the engine has a power input of 5 kW? - Elevator
 The panel house has ten over-ground stories and four underground. The lift goes from the ground floor to the 2nd floor, then down to the 3rd underground floor, nine floors up, and finally four floors down. To what floor does the elevator arrive? How many
The panel house has ten over-ground stories and four underground. The lift goes from the ground floor to the 2nd floor, then down to the 3rd underground floor, nine floors up, and finally four floors down. To what floor does the elevator arrive? How many - Gravitational 12411
 We lift a weight of 2 kg to a height of 50 cm above the top of the table. Determine its gravitational potential energy: a) relative to the tabletop, b) relative to the floor if the table top is 1m above the floor.
We lift a weight of 2 kg to a height of 50 cm above the top of the table. Determine its gravitational potential energy: a) relative to the tabletop, b) relative to the floor if the table top is 1m above the floor. - Car
 At what horizontal distance reaches the car weight m = 753 kg speed v = 74 km/h when the car engine develops a tensile force F = 3061 N. (Neglect resistance of the environment.)
At what horizontal distance reaches the car weight m = 753 kg speed v = 74 km/h when the car engine develops a tensile force F = 3061 N. (Neglect resistance of the environment.) - The elevator
 The elevator car weighing 400 kg rises from the third to the fifth floor. By what value will the potential gravitational energy of the cabin increase? What useful work will the elevator motor do? The height of one floor is 5m.
The elevator car weighing 400 kg rises from the third to the fifth floor. By what value will the potential gravitational energy of the cabin increase? What useful work will the elevator motor do? The height of one floor is 5m. - Newton law
 At what acceleration moves a train with a weight of 800 t start if the traction force of the locomotive is 2 * 105 N?
At what acceleration moves a train with a weight of 800 t start if the traction force of the locomotive is 2 * 105 N? - The elevator
 Hanka took the elevator. She got on the third floor, went down to the basement, went up five stories, went down two floors, up three, up two again, and got out. On which floor did she get off? (Don't forget what the basement is)
Hanka took the elevator. She got on the third floor, went down to the basement, went up five stories, went down two floors, up three, up two again, and got out. On which floor did she get off? (Don't forget what the basement is) - Temperature 7595
 Colorless liquid weighing m = 200 g is heated with constant stirring on a stove with power input P0 = 600W. 80% of the supplied energy is used to heat the liquid. Selected measured values of liquid temperature as a function of time are recorded in the t
Colorless liquid weighing m = 200 g is heated with constant stirring on a stove with power input P0 = 600W. 80% of the supplied energy is used to heat the liquid. Selected measured values of liquid temperature as a function of time are recorded in the t - Chained winch
 When digging a well, a chained winch balances the material. An empty shackle weighs 8 kg, a total of 64 kg. What force must the worker exert on the crank handle when pulling the shackle with a constant movement from a depth of 5 m if the shaft diameter is
When digging a well, a chained winch balances the material. An empty shackle weighs 8 kg, a total of 64 kg. What force must the worker exert on the crank handle when pulling the shackle with a constant movement from a depth of 5 m if the shaft diameter is - Kilometers 8362
 The cyclist left place A at 8:00 a.m. at a constant speed of 25 km/h. At 8:30, a passenger car leaves A at a speed of 75 km/h along the same route. How many kilometers does the cyclist travel before the car catches up with him?
The cyclist left place A at 8:00 a.m. at a constant speed of 25 km/h. At 8:30, a passenger car leaves A at a speed of 75 km/h along the same route. How many kilometers does the cyclist travel before the car catches up with him? - Fuel efficiency
 The gravimetric analysis of an anthracite fuel is 90% carbon, 3% hydrogen, 2% oxygen, and 1% nitrogen. Given that analysis of the dry combustion products by volume is 16.2% CO2, 3.5% O2, and 80.3% N2, during the combustion process of anthracite, which con
The gravimetric analysis of an anthracite fuel is 90% carbon, 3% hydrogen, 2% oxygen, and 1% nitrogen. Given that analysis of the dry combustion products by volume is 16.2% CO2, 3.5% O2, and 80.3% N2, during the combustion process of anthracite, which con - Straightened 26861
 A Mazda van with a box body with internal dimensions of 1.6 m x 3.1 m x 1.7 m (w x d x h) with a payload of 1.7 tons delivers crates with pastries. Pastry box 520: dimensions 600mm x 400mm x 200mm (l x w x h), load capacity 15 kg. Calculate: a) How many c
A Mazda van with a box body with internal dimensions of 1.6 m x 3.1 m x 1.7 m (w x d x h) with a payload of 1.7 tons delivers crates with pastries. Pastry box 520: dimensions 600mm x 400mm x 200mm (l x w x h), load capacity 15 kg. Calculate: a) How many c - Water container
 The container with water weighs 1.48 kg when we cast 75% of the water content of water weight 0.73 kg. How heavy is an empty container?
The container with water weighs 1.48 kg when we cast 75% of the water content of water weight 0.73 kg. How heavy is an empty container? - Barrel with liquid
 Barrel with grain weight 297 kg. When it sheds 48% of grain, ha weight 174 kg, what is the weight of an empty barrel?
Barrel with grain weight 297 kg. When it sheds 48% of grain, ha weight 174 kg, what is the weight of an empty barrel? - Potential 42561
 The elevator cabin weighing 720 kg goes from the ground floor to the top floor of the building, at 125 m. How much potential energy does the elevator cabin have on the top floor of the building - at the height of 125 m?
The elevator cabin weighing 720 kg goes from the ground floor to the top floor of the building, at 125 m. How much potential energy does the elevator cabin have on the top floor of the building - at the height of 125 m? - Equilibrium 7990
 At the end of one arm of the equilibrium scales, which are in equilibrium, a lead body with a volume V1 is suspended in the air. At the end of the other arm is an aluminum body with a volume of V2. The balance arms have sizes l1 and l2, lead density h1 =
At the end of one arm of the equilibrium scales, which are in equilibrium, a lead body with a volume V1 is suspended in the air. At the end of the other arm is an aluminum body with a volume of V2. The balance arms have sizes l1 and l2, lead density h1 =
