Cans
How many cans must be put in the bottom row if we want 182 cans arranged in 13 rows above so that each subsequent row has always been one in less? How many cans will be in the top row?
Correct answer:
Tips for related online calculators
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Subsequent 6477
We will put 900 bags in 9 rows so that there are five fewer in each subsequent one. How much is in the first place? - Tower
Charles built a tower of cubes with an edge 2 cm long. In the lowest layer, there were six cubes (in one row) in six rows. In each subsequent layer, always one cube and one row less. What volume in cm³ did the whole tower have? - Arranged 80453
There are 390 trees arranged in rows in the orchard. How many rows are there if each row has the same number of trees greater than 30 and less than 40? - Triangle of cans
A display of cans on a grocery shelf consists of 28 cans at the bottom, 25 cans in the next row, and so on. There are nine rows on a shelf. How many cans are there in the 9th row? How many cans in total are on display? - Cinema
How many rows of seats are in the stands if you know that the first row has 24 seats and the last 50 seats, and each subsequent row has two more seats than the row before? How many seats are in the stands? - Roof
Tiles are stacked in rows on the trapezoidal-shaped roof. At the ridge are 15 tiles, and each subsequent row has one more tile than the previous row. How many tiles are covered the roof if the lowermost row has 37 tiles? - Seats
Seats in the sports hall are organized so that each subsequent row has five more seats. The First has ten seats. How many seats are: a) in the eighth row b) in the eighteenth row - Highest 62464
The iron pipes are placed in 10 rows, one above the other so that in the highest upper row, there are 15 pipes, and in each other, there is one tube more. How many pipes are there? - Spectators 82430
In a circus, in one sector for spectators, the seats are arranged in such a way that in each higher row, there is one more seat than in the previous one. How many seats are there in a sector with 22 rows if there are 8 seats in the first row? - Coin
How many 20-cent coins must be put in a row that the next 20-cent coins after them (above) rolled on its axis? - Tubes
Iron tubes in the warehouse are stored in layers so that each tube's top layer fits into the gaps of the lower layer. How many layers are needed to deposit 100 tubes if the top layer has 9 tubes? How many tubes are in the bottom layer of tubes? - Subsequent 82511
The theater has 20 rows of seats on the ground floor. There are 16 seats in the first row, and each subsequent row has two more seats than the previous one. Find the number of seats on the ground floor of the theater. - Restriction 7442
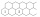The figure shows two rows of hexagonal boxes that continue to the right without restriction. Fill in one field with one positive integer so that the product of the numbers in any three adjacent fields is 2018. Determine the number that will be in the top - Ninety-one 80354
Ninety-one books are arranged on seven shelves so that there are 4 more books on each subsequent shelf than on the previous one. How many books are on the 7th shelf? - Book Store
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Collected 38381
The foreman collected 268 kg of apples and must sort them into baskets of 7 kg each. Can they divide the apples correctly? Will all baskets be refilled? How many baskets will they need if they want to put all the apples in the baskets? - Boxes
Two hundred boxes have been straightened in three rows. The first row was 13 more than in the second, and the second was one-fifth more than in the third. How many boxes are in each row?
