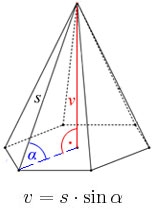
Hexagonal pyramid
Regular hexagonal pyramid has dimensions: length edge of the base a = 1.8 dm and the height of the pyramid = 2.4 dm. Calculate the surface area and volume of a pyramid.
Correct answer:
Tips for related online calculators
See also our right triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- solid geometry
- pyramid
- surface area
- planimetrics
- Pythagorean theorem
- right triangle
- polygon
- area of a shape
- triangle
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Quadrilateral pyramid
 A regular quadrilateral pyramid has a volume of 24 dm³ and a base edge a = 4 dm. Calculate: a/height of the pyramid b/sidewall height c/surface of the pyramid
A regular quadrilateral pyramid has a volume of 24 dm³ and a base edge a = 4 dm. Calculate: a/height of the pyramid b/sidewall height c/surface of the pyramid - Hexagonal prism
 Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm.
Calculate the volume and surface of a regular hexagonal prism with the edge of the base a = 6 cm with the corresponding height v1 = 5.2cm and the height of the prism h = 1 dm. - Hexaprism container
 Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm.
Calculate the volume and surface in the shape of a regular hexagonal prism with a height of 1.4 m, a base edge of 3dm, and a corresponding height of 2.6 dm. - Hexagonal pyramid
 Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
Calculate the volume and the surface of a regular hexagonal pyramid with a base edge length of 3 cm and a height of 5 cm.
- Hexagonal pyramid
 Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m.
Calculate a regular hexagonal pyramid's volume and surface area with a base edge a = 30 m and a side edge b = 50 m. - Quadrilateral 44561
 The regular quadrilateral pyramid has a volume of 212 m³ and a base edge a = 7.2 m. Calculate the surface area and height of the pyramid.
The regular quadrilateral pyramid has a volume of 212 m³ and a base edge a = 7.2 m. Calculate the surface area and height of the pyramid. - Calculation 81401
 A regular four-sided pyramid has a volume of 2,160 liters and a base edge length of 12 dm. Calculate the height of the needle (sketch, calculation, answer).
A regular four-sided pyramid has a volume of 2,160 liters and a base edge length of 12 dm. Calculate the height of the needle (sketch, calculation, answer). - Calculate 6331
 The regular hexagonal pyramid has a base edge of 20 cm and a side edge of 40 cm. Calculate the height and surface of the pyramid
The regular hexagonal pyramid has a base edge of 20 cm and a side edge of 40 cm. Calculate the height and surface of the pyramid - Calculate 66254
 Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
Calculate the volume and surface of a regular hexagonal prism with a height v = 2cm and a base edge a = 8cm.
- Quadrilateral 6116
 The area of the mantle of a regular quadrilateral pyramid is equal to twice the area of its base. Calculate the pyramid's surface if the length of the base edge is 20 dm.
The area of the mantle of a regular quadrilateral pyramid is equal to twice the area of its base. Calculate the pyramid's surface if the length of the base edge is 20 dm. - Consumption 17823
 The roof has the shape of a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses.
The roof has the shape of a regular hexagonal pyramid shell with a wall height of v = 5 m and a base edge of a = 4 m. Calculate the consumption of sheet metal to cover the roof, assuming 15% losses. - Triangular 46641
 The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume.
The regular triangular pyramid ABCDV has a base edge length of 8 cm and a height of 7 cm. Calculate the pyramid's surface area and volume. - Calculate 36263
 Calculate the surface area and volume of a regular 4-sided pyramid with a base edge of a = 12 cm and a height of v = 5 cm
Calculate the surface area and volume of a regular 4-sided pyramid with a base edge of a = 12 cm and a height of v = 5 cm - Quadrilateral pyramid
 We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid
We have a regular quadrilateral pyramid with a base edge a = 10 cm and a height v = 7 cm. Calculate 1/base area 2/casing area 3/pyramid surface 4/volume of the pyramid
- Quadrilateral 7815
 The area of the mantle of a regular quadrilateral pyramid is equal to twice the area of its base. Calculate the pyramid's volume if the base edge's length is 20 dm.
The area of the mantle of a regular quadrilateral pyramid is equal to twice the area of its base. Calculate the pyramid's volume if the base edge's length is 20 dm. - Hexagonal 13891
 A regular hexagonal pyramid has a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. Please sketch the picture. Please calculate the surface of a regular hexagonal pyramid.
A regular hexagonal pyramid has a base inscribed in a circle with a radius of 8 cm and a height of 20 cm. Please sketch the picture. Please calculate the surface of a regular hexagonal pyramid. - Surface of pyramid
 A regular quadrilateral pyramid has the height of the sidewall equal to the length of the edge of the base. The area of the sidewall is 32 cm². What is the surface of the pyramid?
A regular quadrilateral pyramid has the height of the sidewall equal to the length of the edge of the base. The area of the sidewall is 32 cm². What is the surface of the pyramid?
