Mrak - cloud
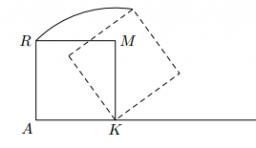
It is given segment AB of length 12 cm, where one side of the square MRAK is laid on it. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB the point R leaves a paper trail.
Draw the whole track of point R until the square can do the line AB on both sides and returns to its original position.
Draw the whole track of point R until the square can do the line AB on both sides and returns to its original position.
Correct answer:
You need to know the following knowledge to solve this word math problem:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- RST triangle
 Find out if it is possible to construct the given triangle and according to which theorem: RS = 2.5 cm ST = 7 cm TR = 4.5 cm
Find out if it is possible to construct the given triangle and according to which theorem: RS = 2.5 cm ST = 7 cm TR = 4.5 cm - Prove 2
 Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7).
Prove that the minimum number of straight single cuts/strokes needs to divide a given right-angled triangle or an obtuse-angled triangle into a collection of all acute-angled triangles is seven(7). - Sss triangle 2
 Construct triangle ABC in which |AB|=5cm, |AC|=6cm and |BC|=9cm
Construct triangle ABC in which |AB|=5cm, |AC|=6cm and |BC|=9cm - Triangle 73464
 The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
The given line is a BC length of 6 cm. Construct a triangle so that the BAC angle is 50° and the height to the side is 5.5 cm. Thank you very much.
- Trapezoid 70454
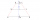 Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60°
Construct a trapezoid ABCD (AB // CD): | AB | = 7cm | BC | = 3.5cm | CD | = 4cm The magnitude of the angle ABC = 60° - Shortest walk
 An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point
An ant is crawling around this cube. The cube is made of wire. Each side of the cube is 3 inches long. (Those sides are called edges.) Points A and B are vertices of the cube. What is the least distance the ant would have to crawl if it starts from point - Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Construct 61253
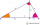 Using Euclid's theorem, construct a line of length √15.
Using Euclid's theorem, construct a line of length √15. - Draw triangle
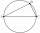 Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
- Number line
 Visualize and color the following decimal numbers using a grid. 1. 0.35 2. 1.9 3. 0.45 4. 1.15 5. 0.8
Visualize and color the following decimal numbers using a grid. 1. 0.35 2. 1.9 3. 0.45 4. 1.15 5. 0.8 - Draw SSA triangle
 Draw a triangle ABC if you know: alpha = 60° side b = 4 cm side a = 10 cm
Draw a triangle ABC if you know: alpha = 60° side b = 4 cm side a = 10 cm - Construct
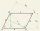 Construct a rhombus ABCD with side a = 7cm, b = 5cm, whose diagonal e is perpendicular to side b.
Construct a rhombus ABCD with side a = 7cm, b = 5cm, whose diagonal e is perpendicular to side b. - Square equal rhombus
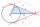 Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm and angle |DAB| = 30°.
Construct a square that has the same area as a rhombus ABCD if |AB| = 5cm, |AD| = 4cm and angle |DAB| = 30°. - Divide an isosceles triangle
 How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
How to divide an isosceles triangle into two parts with equal areas perpendicular to the axis of symmetry (into a trapezoid and a triangle)?
- As shown
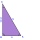 As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6, then the perimeter of △ BDE
As shown, in △ ABC, ∠C = 90°, AD bisects ∠BAC, DE⊥AB to E, BE = 2, BC = 6, then the perimeter of △ BDE - Vertex points
 Suppose the following points of a triangle: P(-12,6), Q(4,0), R(-8,-6). Graph the triangle. Find the triangle area.
Suppose the following points of a triangle: P(-12,6), Q(4,0), R(-8,-6). Graph the triangle. Find the triangle area. - Construction
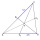 Construct the triangle ABC if you know: the size of the side AC is 6 cm, the size of the angle ACB is 60°, and the distance of the center of gravity T from the vertex A is 4 cm. (Sketch, analysis, notation of construction, construction)
Construct the triangle ABC if you know: the size of the side AC is 6 cm, the size of the angle ACB is 60°, and the distance of the center of gravity T from the vertex A is 4 cm. (Sketch, analysis, notation of construction, construction)
