Hypotenuse and height
In a right triangle is length of the hypotenuse c = 56 cm and height hc = 4 cm. Determine the length of both triangle legs.
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- planimetrics
- right triangle
- triangle
- The right triangle altitude theorem
- numbers
- real numbers
Units of physical quantities:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Quadrilateral 78874
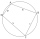 Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime
Given is a quadrilateral ABCD inscribed in a circle, with the diagonal AC being the circle's diameter. The distance between point B and the diameter is 15 cm, and between point D and the diameter is 18 cm. Calculate the radius of the circle and the perime - Construct 61253
 Using Euclid's theorem, construct a line of length √15.
Using Euclid's theorem, construct a line of length √15. - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - MIT 1869
 You know the length of hypotenuse parts 9 and 16, at which the hypotenuse of a right triangle is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts Inst
You know the length of hypotenuse parts 9 and 16, at which the hypotenuse of a right triangle is divided by a height. The task is to find the lengths of the sides of the triangle and the length of line x. This assignment was part of the Massachusetts Inst - Height of right RT
 The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle?
The right triangle ABC has a hypotenuse c 9 cm long and a part of the hypotenuse cb = 3 cm. How long is the height of this right triangle? - Right triangle - ratio
 The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle.
The lengths of the legs of the right triangle ABC are in ratio b = 2:3. The hypotenuse is 10 cm long. Calculate the lengths of the legs of that triangle. - RT triangle and height
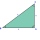 Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm.
Calculate the remaining sides of the right triangle if we know side b = 4 cm long and height to side c h = 2.4 cm. - Free space in the garden
 The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows
The grandfather's free space in the garden was in the shape of a rectangular triangle of 5 meters and 12 meters in length. He decided to divide it into two parts and the height of the hypotenuse. The smaller part creates a rock garden, for the larger sows - Squares above sides
 Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc
Two squares are constructed on two sides of the ABC triangle. The square area above the BC side is 25 cm². The height vc to the side AB is 3 cm long. The heel P of height vc divides the AB side in a 2: 1 ratio. The AC side is longer than the BC side. Calc - Medians in right triangle
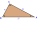 It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides?
It is given a right triangle, and angle C is 90 degrees. I know it medians t1 = 8 cm and median t2 = 12 cm. How to calculate the length of the sides? - Isosceles triangle 9
 There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle.
There is an isosceles triangle ABC where AB= AC. The perimeter is 64cm, and the altitude is 24cm. Find the area of the isosceles triangle. - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Right isosceles triangle
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two equal segments. The length of one segment is 5 cm. What is the area of the triangle?
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two equal segments. The length of one segment is 5 cm. What is the area of the triangle? - Right 24
 The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two unequal segments. The length of one segment is 5 cm. What is the area of the triangle? Thank you.
The right isosceles triangle has an altitude x drawn from the right angle to the hypotenuse dividing it into two unequal segments. The length of one segment is 5 cm. What is the area of the triangle? Thank you. - Same area
 There is a given triangle. Construct a square of the same area.
There is a given triangle. Construct a square of the same area. - Hypotenuse - RT
 A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle?
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Conical area
 A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
A right-angled triangle has sides a=12 and b=19 at the right angle. The hypotenuse is c. If the triangle rotates on the c side as an axis, find the volume and surface area of the conical area created by this rotation.
