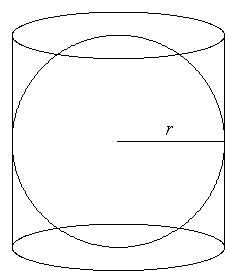
Equilateral cylinder
A sphere is inserted into the rotating equilateral cylinder (touching the bases and the shell). Prove that the cylinder has both a volume and a surface half larger than an inscribed sphere.
Correct answer:
Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Themes, topics:
Grade of the word problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two pots
 Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot
Two similar pots have 16 cm and 10 cm heights if the smaller pot holds 0,75 l. Find the capacity of the larger pot - Two bodies
 The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo
The rectangle with dimensions 8 cm and 4 cm is rotated 360º first around the longer side to form the first body. Then, we similarly rotate the rectangle around the shorter side b to form a second body. Find the ratio of surfaces of the first and second bo - Ratio of volumes
 If the heights of two cylindrical drums are in the ratio 7:8 and their base radii are in the ratio 4:3. What is the ratio of their volumes?
If the heights of two cylindrical drums are in the ratio 7:8 and their base radii are in the ratio 4:3. What is the ratio of their volumes? - Cylinder melted into cuboid
 A circular cylinder has an area of cross-section 56cm², and the height is 10cm. The cylinder is melted into a cuboid with a base area of 16cm². What is the height of the cuboid?
A circular cylinder has an area of cross-section 56cm², and the height is 10cm. The cylinder is melted into a cuboid with a base area of 16cm². What is the height of the cuboid?
- Inscribed 6155
 A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies.
A cylinder with a height equal to half the height of the cone is inscribed in the rotating cone. Find the volume ratio of both bodies. - Lathe
 Calculate the percentage of waste if the cube with 53 cm long edge is lathed to the cylinder with a maximum volume.
Calculate the percentage of waste if the cube with 53 cm long edge is lathed to the cylinder with a maximum volume. - Cylinder surface, volume
 The area of the base and the area of the shell are in the ratio of 3:5. Its height is 5 cm less than the radius of the base. Calculate both surface area and volume.
The area of the base and the area of the shell are in the ratio of 3:5. Its height is 5 cm less than the radius of the base. Calculate both surface area and volume. - Axial section
 The axial section of the cylinder has a diagonal 40 cm. The shell size and base surface are in the ratio 3:2. Calculate the volume and surface area of this cylinder.
The axial section of the cylinder has a diagonal 40 cm. The shell size and base surface are in the ratio 3:2. Calculate the volume and surface area of this cylinder. - Velocity ratio
 Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui
Determine the ratio at which the fluid velocity in different parts of the pipeline (one piece has a diameter of 5 cm and the other has a diameter of 3 cm) when you know that every point of the liquid is the product of the area of the tube [S] and the flui
- Axial section
 The axial section of the cylinder has a diagonal 36 cm long, and we know that the area of the side and the base area is in ratio 1:1. Calculate the height and radius of the cylinder base.
The axial section of the cylinder has a diagonal 36 cm long, and we know that the area of the side and the base area is in ratio 1:1. Calculate the height and radius of the cylinder base. - Scale
 The student drew the cylinder in scale 2:1. How many times is the volume of the cylinder smaller in reality?
The student drew the cylinder in scale 2:1. How many times is the volume of the cylinder smaller in reality? - Lathe
 From the cube of edge, 37 cm was a lathed maximum cylinder. What percentage of the cube is left as waste after being lathed?
From the cube of edge, 37 cm was a lathed maximum cylinder. What percentage of the cube is left as waste after being lathed? - Gutter
 How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material.
How much metal is needed to produce 60 pieces of gutter pipes with the diameter 17 cm and length of 6 m? The plate bends add 6% of the material. - Pipes
 The water pipe has a cross-section 1184 cm². An hour has passed 743 m³ of water. How much water flows through the pipe with cross-section 300 cm² per 6 hours if water flows at the same speed?
The water pipe has a cross-section 1184 cm². An hour has passed 743 m³ of water. How much water flows through the pipe with cross-section 300 cm² per 6 hours if water flows at the same speed?
- Cone in cylinder
 The cylinder is an inscribed cone. Find the ratio of the volume of the cone and cylinder. Please write the ratio as a decimal number and as a percentage.
The cylinder is an inscribed cone. Find the ratio of the volume of the cone and cylinder. Please write the ratio as a decimal number and as a percentage. - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The number 10
 The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
The number of sides of two regular polygons differ by 1 the sum of the interior angles of the polygons is in the ratio of 3:2 calculate the number of sides of each polygon.
