Two rectangles
I cut out two rectangles with 54 cm² and 90 cm². Their sides are expressed in whole centimeters. If I put these rectangles together, I get a rectangle with an area of 144 cm2. What dimensions can this large rectangle have? Write all options. Explain your calculation.
Correct answer:

Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Two-digit 82521
 Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned?
Karel had to multiply two two-digit numbers. Out of care, he changed the order of the digits in one of the factors and got a product that was 4,248 less than the correct result. What is the correct result? How much should Karl have earned? - Grandma
 Grandma is 57 years older than her two twin granddaughters. If we add the ages of an older woman with both granddaughters, we get the number 99. How old is her old woman?
Grandma is 57 years older than her two twin granddaughters. If we add the ages of an older woman with both granddaughters, we get the number 99. How old is her old woman? - The isosceles
 The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid?
The isosceles trapezoid ABCD has bases of 18 cm and 12 cm. The angle at apex A is 60°. What is the circumference and area of the trapezoid? - Phone number
 Ivan's phone number ends with a four-digit number: When we subtract the first from the fourth digit of this four-digit number, we get the same number as when we subtract the second from the third digit. If we write the four-digit number from the back and
Ivan's phone number ends with a four-digit number: When we subtract the first from the fourth digit of this four-digit number, we get the same number as when we subtract the second from the third digit. If we write the four-digit number from the back and
- Five-digit number
 Anna thinks of a five-digit number not divisible by three or four. If he increments each digit by one, it gets a five-digit number divisible by three. If he reduces each digit by one, he gets a five-digit number divisible by four. If it swaps any two digi
Anna thinks of a five-digit number not divisible by three or four. If he increments each digit by one, it gets a five-digit number divisible by three. If he reduces each digit by one, he gets a five-digit number divisible by four. If it swaps any two digi - All pairs
 Find all pairs (m, n) of natural numbers for which is true: m s (n) = n s (m) = 70, where s(a) denotes the digit sum of the natural number a.
Find all pairs (m, n) of natural numbers for which is true: m s (n) = n s (m) = 70, where s(a) denotes the digit sum of the natural number a. - Candles
 Before Christmas, Eva bought two cylindrical candles - red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM, lit a green candle at 7:00 PM, and left them on fire until it burned. At 9:30 PM, both candles were the
Before Christmas, Eva bought two cylindrical candles - red and green. Red was 1 cm longer than green. She lit a red candle on Christmas Day at 5:30 PM, lit a green candle at 7:00 PM, and left them on fire until it burned. At 9:30 PM, both candles were the - Apples and pears
 Apples cost 50 cents a piece, pears 60 cents a piece, bananas cheaper than pears. Grandma bought five pieces of fruit. There was only one banana, and I paid 2 euros 75 cents. How many apples and how many pears?
Apples cost 50 cents a piece, pears 60 cents a piece, bananas cheaper than pears. Grandma bought five pieces of fruit. There was only one banana, and I paid 2 euros 75 cents. How many apples and how many pears? - Two cars on ring
 There were two cars on the round track (ring) in the adjacent tracks, the first car on the inner track and the second on the outer track. Both cars started at the same time from one starting track. The first toy car drove four laps simultaneously, and the
There were two cars on the round track (ring) in the adjacent tracks, the first car on the inner track and the second on the outer track. Both cars started at the same time from one starting track. The first toy car drove four laps simultaneously, and the
- Self-counting machine
 The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he
The self-counting machine works exactly like a calculator. The innkeeper wanted to add several three-digit natural numbers on his own. On the first attempt, he got the result in 2224. To check, he added these numbers again, and he got 2198. Therefore, he - Equilateral triangle ABC
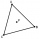 In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - Special watch
 Fero bought a special watch on the market. They have only one (minute) hand and a display showing the angle between the hour and minute hand. How many hours was his watch shown - the minute hand points to number 2; the display shows 125°.
Fero bought a special watch on the market. They have only one (minute) hand and a display showing the angle between the hour and minute hand. How many hours was his watch shown - the minute hand points to number 2; the display shows 125°. - Triplets
 Three years ago, the triplets Pavel, Petr, Luke, and their five-year-old sister Jane had been together for 25 years. How old is Jane today?
Three years ago, the triplets Pavel, Petr, Luke, and their five-year-old sister Jane had been together for 25 years. How old is Jane today? - Solutions 5453
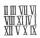 Tongue twister. Replace the letters with numbers to get the correct sum: ŠKRZ KRK STRČ ______ PRST How many solutions does the task have?
Tongue twister. Replace the letters with numbers to get the correct sum: ŠKRZ KRK STRČ ______ PRST How many solutions does the task have?
- One million
 Write the million number (1000000) using only nine numbers and algebraic operations plus, minus, times, divided, powers, and squares. Find at least three different solutions.
Write the million number (1000000) using only nine numbers and algebraic operations plus, minus, times, divided, powers, and squares. Find at least three different solutions. - Equation algebraogram
 Solve the equation: oco + ivo = cita How much has the task of solutions?
Solve the equation: oco + ivo = cita How much has the task of solutions? - Alarm clock
 The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
The old watchmaker has a unique digital alarm in its collection that rings whenever the sum of the alarm's digits equals 21. Find out when the alarm clock will ring. What is their number? List all options.
