Count of triangles
On each side of an ABCD square is 10 internal points.
Determine the number of triangles with vertices at these points.
Determine the number of triangles with vertices at these points.
Correct answer:

Tips for related online calculators
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- In an
 In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square.
In an ABCD square, n interior points are chosen on each side. Find the number of all triangles whose vertices X, Y, and Z lie at these points and on different sides of the square. - N points on the side
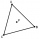 An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides.
An equilateral triangle A, B, and C on each of its inner sides lies N=13 points. Find the number of all triangles whose vertices lie at given points on different sides. - Combi-triangle
 Each square side is marked 10 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square?
Each square side is marked 10 different points outside the square's vertices. How many triangles can be constructed from this set of points, where each vertex of the triangle lies on the other side of the square? - Internal angles
 The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det
The ABCD is an isosceles trapezoid, which holds: |AB| = 2 |BC| = 2 |CD| = 2 |DA|: On the BC side is a K point such that |BK| = 2 |KC|, on its side CD is the point L such that |CL| = 2 |LD|, and on its side DA, the point M is such that | DM | = 2 |MA|. Det - Construct 30121
 Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB
Point B is a vertex of rectangle ABCD. The diagonal BD of this rectangle lies on the line p. Point X is an interior point of side AD of rectangle ABCD, and point Y is an internal point of side CD. Construct the missing vertices D, A, and C of rectangle AB - Different 42191
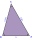 How many different triangles with vertices formed by points A, B, C, D, E, and F can we create?
How many different triangles with vertices formed by points A, B, C, D, E, and F can we create? - Square 2
 Points D[10,-8] and B[4,5] are opposed vertices of the square ABCD. Calculate the area of the square ABCD.
Points D[10,-8] and B[4,5] are opposed vertices of the square ABCD. Calculate the area of the square ABCD. - Coordinates of the intersection of the diagonals
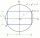 In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle.
In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle. - Intersection 3383
 A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate
A regular 15-angle is given. A triangle is formed if we connect points 3 and 7, 13 and 10. The vertices are 3 and 13, and the lines' intersections are 3.7 and 13.10. We are to determine the angle size formed by sides 3.7 and 13.10. These numbers indicate - Right-angled 66344
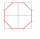 From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm².
From a square with a side of 4 cm, we cut four right-angled isosceles triangles with right angles at the square's vertices and with an overlap of √2 cm. We get an octagon. Calculate its perimeter if the area of the octagon is 14 cm². - Rectangle - parallelogram
 A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle.
A rectangle is circumscribed by a circle with a radius of 5 cm. The short side of the rectangle measures 6 cm. Calculate the perimeter of a parallelogram ABCD, whose vertices are the midpoints of the sides of the rectangle. - Respectively 81293
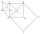 The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help...
The figure shows the squares ABCD, EFCA, CHCE, and IJHE. Points S, B, F, and G are, respectively, the centers of these squares. Line segment AC is 1 cm long. Determine the area of triangle IJS. Please help... - Surveyors
 Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other?
Surveyors mark 4 points on the globe's surface so their distances are the same. What is their distance from each other? - Circle and square
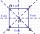 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Hexagon - MO
 The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and is true |DJ|
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and is true |DJ| - Similarity of squares
 The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than an area of a square ABCD with side a: ...
The ratio of the similarity of the squares ABCD and KLMN is 2.5. Square KLMN area is greater than an area of a square ABCD with side a: ... - Similarity coefficient
 In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other.
In the triangle TMA, the length of the sides is t = 5cm, m = 3.5cm, and a = 6.2cm. Another similar triangle has side lengths of 6.65 cm, 11.78 cm, and 9.5 cm. Determine the similarity coefficient of these triangles and assign similar sides to each other.
