Clock
How many times a day do hands on a clock overlap?
Correct answer:

Showing 1 comment:
Tips for related online calculators
Need help calculating sum, simplifying, or multiplying fractions? Try our fraction calculator.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Check out our ratio calculator.
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert velocity (speed) units?
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Our percentage calculator will help you quickly calculate various typical tasks with percentages.
Check out our ratio calculator.
Do you solve Diofant problems and looking for a calculator of Diofant integer equations?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Do you want to convert length units?
Do you want to convert velocity (speed) units?
Do you want to round the number?
Do you want to convert time units like minutes to seconds?
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- algebra
- equation
- integer equation
- arithmetic
- division
- rounding
- planimetrics
- circle
- basic functions
- ratio
- percentages
- modulo
- numbers
- fractions
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Lunes of Hippocrates
 Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the
Calculate the sum of the area of the so-called Hippocratic lunas, which were cut above the legs of a right triangle (a = 6cm, b = 8cm). Instructions: First, calculate the area of the semicircles above all sides of the ABC triangle. Compare the sum of the - Draw triangle
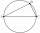 Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37°
Construct right triangle MNO with hypotenuse o = 5 cm and angle MNO = 37° - Touch circle
 Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l
Point A has a distance (A, k) = 10 cm from a circle k with radius r = 4 cm and center S. Calculate: a) the distance of point A from the point of contact T if the tangent to the circle is drawn from point A b) the distance of the contact point T from the l - The amphitheater
 The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which of the spectators, P, Q, R, S, T, sees the stage at the greatest viewing angle?
The amphitheater has the shape of a semicircle, the spectators sit on the perimeter of the semicircle, and the stage forms the diameter of the semicircle. Which of the spectators, P, Q, R, S, T, sees the stage at the greatest viewing angle? - Construct rhombus
 Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm
Construct rhombus ABCD if given diagonal length | AC | = 8cm, inscribed circle radius r = 1.5cm - Parallels and one secant
 There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time.
There are two different parallel lines, a, b, and line c, that intersect the two parallel lines. Draw a circle that touches all lines at the same time. - Circle described
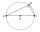 The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle.
The circle radius described in the right triangle with a 6 cm long leg is 5 cm. Calculate the circumference of this triangle. - Two heights and a side
 Construct triangle ABC when the given side is c = 7 cm, height to side a va = 5 cm, and height to side b: vb = 4 cm.
Construct triangle ABC when the given side is c = 7 cm, height to side a va = 5 cm, and height to side b: vb = 4 cm. - Same area
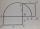 There is a given triangle. Construct a square of the same area.
There is a given triangle. Construct a square of the same area. - Hypotenuse - RT
 A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle?
A triangle has a hypotenuse of 55 and an altitude to the hypotenuse of 33. What is the area of the triangle? - Circle tangent
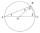 It is given to a circle with the center S and a radius of 3.5 cm. The distance from the center to line p is 6 cm. Construct a circle tangent n which is perpendicular to the line p.
It is given to a circle with the center S and a radius of 3.5 cm. The distance from the center to line p is 6 cm. Construct a circle tangent n which is perpendicular to the line p. - Complete construction
 Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs.
Construct triangle ABC if hypotenuse c = 7 cm and angle ABC = 30 degrees. / Use Thales' theorem - circle /. Measure and write down the length of the legs. - Tangents construct
 The circle k is given k (S; 2.5 cm) and an outer line p. Construct a tangent t of the circle that has a line p angle 60°. How many solutions have the task?
The circle k is given k (S; 2.5 cm) and an outer line p. Construct a tangent t of the circle that has a line p angle 60°. How many solutions have the task? - Inscribed triangle
 To a circle is an inscribed triangle so that it is vertexes divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle.
To a circle is an inscribed triangle so that it is vertexes divide the circle into three arcs. The length of the arcs is in the ratio 2:3:7. Find the interior angles of a triangle. - Right triangle
 Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC.
Draw a right triangle ABC if |AB| = 5 cm |BC| = 3 cm, |AC| = 4 cm. Draw Thales circle above the hypotenuse of the triangle ABC. - The chord
 A chord passing through its center is the side of the triangle inscribed in a circle. What size are the internal angles of a triangle if one of them is 40°?
A chord passing through its center is the side of the triangle inscribed in a circle. What size are the internal angles of a triangle if one of them is 40°? - The bridge
 Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen see the bridge from the largest angle?
Across the circle, the lake passes through its center bridge over the lake. At three different locations on the lakeshore are three fishermen, A, B, and C. Which of the fishermen see the bridge from the largest angle?
