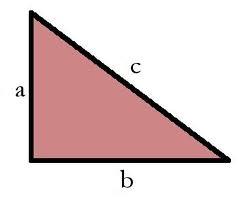
RT and circles
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=23.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Grade of the word problem:
Related math problems and questions:
- Regular n-gon
 Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm?
Which regular polygon has a radius of circumscribed circle r = 10 cm and the radius of inscribed circle p = 9.962 cm? - Annular area
 The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area.
The square with side a = 1 is inscribed and circumscribed by circles. Find the annular area. - Annulus from triangle
 Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm
Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm - Circumscribed 63824
 In a regular decagon, the diameter of the circumscribed circle measures 10 cm. Determine the radius of the circle inscribed in this triangle.
In a regular decagon, the diameter of the circumscribed circle measures 10 cm. Determine the radius of the circle inscribed in this triangle. - Diagonals of pentagon
 Calculate the diagonal length of the regular pentagon: a) inscribed in a circle of radius 12dm; b) a circumscribed circle with a radius of 12dm.
Calculate the diagonal length of the regular pentagon: a) inscribed in a circle of radius 12dm; b) a circumscribed circle with a radius of 12dm. - Dodecagon
 Find the area of a regular dodecagon (n=12) if the radius of the circumscribed circle is 5 cm.
Find the area of a regular dodecagon (n=12) if the radius of the circumscribed circle is 5 cm. - Circumscribed 22713
 Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm.
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Circle inscribed
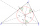 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - Calculate 16223
 The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle).
The following elements are known in the right triangle ABC: a = 10 cm, height to side c h = 9.23 cm. Calculate o, R (radius of the inscribed circle), r (radius of the inscribed circle). - Circumscribed 29561
 Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given.
Construct an isosceles triangle if a given circle circumscribed with a radius r = 2.6 cm is given. - Circumscription
 Calculate the radius of the Circumscribed circle in the rectangle with sides 20 and 19. Can it be a rectangle inscribed by a circle?
Calculate the radius of the Circumscribed circle in the rectangle with sides 20 and 19. Can it be a rectangle inscribed by a circle? - Isosceles IV
 In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle.
In an isosceles triangle ABC is |AC| = |BC| = 13 and |AB| = 10. Calculate the radius of the inscribed (r) and described (R) circle. - Nine-sided 36071
 Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm
Calculate the surface area and volume of a regular nine-sided pyramid if the radius of the circle inscribed in the base measures ρ = 12 cm and the height of the pyramid is 24 cm - Hexagon A
 Calculate the area of a regular hexagon inscribed in a circle with radius r=9 cm.
Calculate the area of a regular hexagon inscribed in a circle with radius r=9 cm. - Circumscribed 81759
 In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle.
In triangle ABC, we know a = 4 cm, b = 6 cm, γ = 60°. Calculate the area and radius of the inscribed and circumscribed circle. - Circumscribed 7290
 Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm.
Calculate the area of a regular hexagon if the radius of the circle circumscribed is 6.8 cm. - N-gon II
 What is the side length of the regular 9-gon circumscribed circle of radius 13 cm?
What is the side length of the regular 9-gon circumscribed circle of radius 13 cm?
