Angle + cosine - practice problems
Number of problems found: 234
- Let z 2
 Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3
Let z = 2 - sqrt(3i). Find z6 and express your answer in rectangular form. if z = 2 - 2sqrt(3 i) then r = |z| = sqrt(2 ^ 2 + (- 2sqrt(3)) ^ 2) = sqrt(16) = 4 and theta = tan -2√3/2=-π/3 - Trigonometric fx
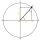 When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ.
When an acute angle φ is in the standard position, its terminal side passes through point P (1,3). Find trigonometric functions of angle θ : sin φ, cos φ, tan φ, cotan φ. - Three 235
 Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B.
Three houses form a triangular shape. House A is 50 feet from house C and house B is 60 feet from house C. The measure is angle ABC is 80 degrees. Draw a picture and find the distance between A and B. - Conjugate coordinates
 If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y.
If the rectangular conjugate of the polar vector 12 angle 35 degrees is equal to x+yi, find the sum of x and y. - Subtract polar forms
 Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form
Solve the following 5.2∠58° - 1.6∠-40° and give answer in polar form - Piece of a wire
 A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is
A piece of wire is bent into the shape of a triangle. Two sides have lengths of 24 inches and 21 inches. The angle between these two sides is 55°. What is the length of the third side to the nearest hundredth of an inch? A: The length of the third side is - A triangle 7
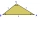 A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c?
A triangle lot has the dimensions a=15m, b=10m, and c=20m. What is the measure of the angle between the sides of b and c? - Using 4
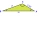 Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15.
Using the law of cosines, find the measurement of leg b if the givens are B=20°, a=10, and c=15. - X-triangle
 Find the length of the x segment in the given triangle drawings.
Find the length of the x segment in the given triangle drawings. - Cotangent
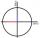 If the angle α is acute, and cotan α = 1/3. Determine the value of sin α, cos α, and tan α.
If the angle α is acute, and cotan α = 1/3. Determine the value of sin α, cos α, and tan α. - Cis notation
 Evaluate multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation.
Evaluate multiplication of two complex numbers in cis notation: (6 cis 120°)(4 cis 30°) Write the result in cis and Re-Im notation. - Resistance 46111
 A metal ring with a radius of 10 cm is placed in a magnetic field so that the normal to its surface makes an angle of 60° with the induction lines. The induction of the magnetic field varies uniformly and drops from 0.45 T to 0.35 T in 0.50 s. Determine t
A metal ring with a radius of 10 cm is placed in a magnetic field so that the normal to its surface makes an angle of 60° with the induction lines. The induction of the magnetic field varies uniformly and drops from 0.45 T to 0.35 T in 0.50 s. Determine t - Perpendicular 17423
 According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta - Scalar dot product
 Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120°
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - Angle between vectors
 Find the angle between the given vectors to the nearest tenth degree. u = (6, 22) and v = (10, -11)
Find the angle between the given vectors to the nearest tenth degree. u = (6, 22) and v = (10, -11) - Two groves
 Two groves A B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'?
Two groves A B are separated by a forest. Both are visible from the hunting grove C, which is connected to both by direct roads. What will be the length of the projected road from A to B if AC = 5004 m, BC = 2600 m, and angle ABC = 53° 45'? - Altitude angles
 Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi
Cities A, B, and C lie in one elevation plane. C is 50 km east of B, and B is north of A. C is deviated by 50° from A. The plane flies around places A, B, and C at the same altitude. When the aircraft is flying around B, its altitude angle to A is 12°. Fi - Two boats
 Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface.
Two boats are located from a height of 150m above the lake's surface at depth angles of 57° and 39°. Find the distance of both boats if the sighting device and both ships are in a plane perpendicular to the lake's surface. - Three pillars
 On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high?
On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high? - Aircraft
 From the aircraft flying at an altitude of 500m, they observed places A and B (at the same altitude) in the direction of flight at depth angles alpha = 48° and beta = 35°. What is the distance between places A and B?
From the aircraft flying at an altitude of 500m, they observed places A and B (at the same altitude) in the direction of flight at depth angles alpha = 48° and beta = 35°. What is the distance between places A and B?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
