Area of a shape + cube - practice problems
Number of problems found: 58
- Chocolate roll
The cube of 5 cm chocolate roll weighs 30 g. How many calories will contain the identical chocolate roller of a prism shape with a length of 0.5 m whose cross-section is an isosceles trapezoid with bases 25 and 13 cm and legs 10 cm? You know that 100 g of - Pyramid cut
We cut the regular square pyramid with a parallel plane to the two parts (see figure). The volume of the smaller pyramid is 20% of the volume of the original one. The bottom of the base of the smaller pyramid has an area of 10 cm². Find the area of the or - Cube cut
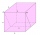In the ABCDA'B'C'D'cube, it is guided by the edge of the CC' a plane witch dividing the cube into two perpendicular four-sided and triangular prisms, whose volumes are 3:2. Determine in which ratio the edge AB is divided by this plane. - The pool
The cube-shaped pool has 140 cubic meters of water. Determine the dimensions of the bottom if the depth of the water is 200 cm and one dimension of the base is 3 m greater than the other. What are the dimensions of the pool bottom? - Considering 67324
Susan has an old stool - a cube with an edge length of 80 cm. She wants to sew a new cover for her. How many square meters does the fabric consume, considering the addition of 15% for stitching and folds? - Milliliters 66834
The cube-shaped vase contains 320 ml of water, which reaches a height of 5 CM. How many milliliters of water can we pour into the vase so that the water does not run out? - Prism
Right-angled prism, whose base is a right triangle with leg a = 3 cm and hypotenuse c = 13 cm, has the same volume as a cube with an edge length of 3 dm. a) Find the height of the prism b) Calculate the surface of the prism c) What percentage of the cube' - The height of prism
The base of the perpendicular prism is formed by a right triangle with perpendiculars 30 cm and 40 cm long. This prism has the same volume as a cube with an edge length of 3 dm. Find its height in cm. - Metal sheet
How much m² of sheet metal is needed to beat a box in the shape of a cube with an edge length of 50 cm, if we add 20% on the folds of the lid and walls? - Calculate 8039
Peter built a cube in Ostrava, each wall with a unique QR code. The edge of the cube is 107 cm long. Calculate how large an area its author had to cover with white and black. - Determine 46401
The volume of the sphere is 20% larger than the volume of the cone. Find its surface if the volume of the cone is 320 cm³. - Original 63974
If we reduce the length of the cube edge by 30%, this cube has a reduced surface area by 1176 cm². Specify the edge length and volume of the original cube. - Calculate 26433
Calculate how much cm² of paper needs to be bought to make a 60 mm cube if you need to add an extra 12% to the folds. - Equilateral cylinder
Equilateral cylinder (height = base diameter; h = 2r) has a volume of V = 199 cm³ . Calculate the surface area of the cylinder. - Needed 5373
The box has the shape of a cube with an edge 52 cm long. How many m² of sheet metal is needed to make a box with a lid? Add 5% to the folds of the lid and walls. - Wallpaper
3750 cm square of wallpaper is needed to glue a cube-shaped box. Can Dad cut out the whole necessary piece of wallpaper as a whole if he has a roll of wallpaper 50 cm wide? - A butter
A butter cube with an edge 6.5 cm long is packed in a package with dimensions a = 28 cm, b = 15 cm. Calculate how many cm² the package is larger than the surface of the cube. - Cutting the prism
A prism with a square base with an area of 1 cm² and a height of 3 cm was cut from a cube with an edge length of 3 cm. What is the body's surface formed from the cube after cutting the prism? - One-quarter 16853 How many m² of paper is needed to produce 1000 pieces of cube-shaped boxes with an edge of 8 cm when we must add one-quarter of the area to the joints?
- Centimeters 68084
The cube-shaped container has a surface area of 320 square centimeters without a lid. Calculate its volume.
Do you have homework that you can't solve? Ask a question, and we try to solve it.
