Area of a shape - practice for 14 year olds - page 11 of 40
Number of problems found: 797
- Calculate 58953
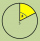 Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °.
Calculate the area of a circular line if the radius r = 80 cm and the central angle is α = 110 °. - Circumscribed 22713
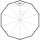 Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm.
Calculate the circumference and the area of a regular ten-angle polygon if the radius of the circumscribed circle r = 20 cm. - Annulus from triangle
 Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm
Calculate the area of the area bounded by a circle circumscribed and a circle inscribed by a triangle with sides a = 25mm, b = 29mm, c = 36mm - Circumference 9211
 The rectangle has a circumference of 30 cm, and its width is 3 cm shorter than its length. What is its area?
The rectangle has a circumference of 30 cm, and its width is 3 cm shorter than its length. What is its area? - Calculate: 6679
 In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c
In the right triangle ABC, we know the right angle γ, the area S = 48 cm2, and the side a = 8 cm. Calculate: pages b, c - Determine 3779
 Determine the perimeter of the rectangle if its length and width are 2:1 and the area is 98 cm².
Determine the perimeter of the rectangle if its length and width are 2:1 and the area is 98 cm². - Inner-circle 2902
 The student should remove the inner circle with a radius of 3 cm from the circle with a radius of 7 cm. How much of the area of the large circle will be removed? Express result in percent.
The student should remove the inner circle with a radius of 3 cm from the circle with a radius of 7 cm. How much of the area of the large circle will be removed? Express result in percent. - Nikelin and brass
 Calculate the length of brass wire (ró=0.08 microohm m) and nickel (ró=0.4 microohm m) with a diameter of 0.5 mm, which has a resistance of 1 ohm
Calculate the length of brass wire (ró=0.08 microohm m) and nickel (ró=0.4 microohm m) with a diameter of 0.5 mm, which has a resistance of 1 ohm - Ratio of triangles areas
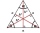 In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas
In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - An equilateral
 An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle?
An equilateral triangle is inscribed in a square of side 1 unit long so that it has one common vertex with the square. What is the area of the inscribed triangle? - Rectangular garden
 The perimeter of Peter's rectangular garden is 98 meters. The width of the garden is 60% shorter than its length. Find the dimensions of the rectangular garden in meters. Find the garden area in square meters.
The perimeter of Peter's rectangular garden is 98 meters. The width of the garden is 60% shorter than its length. Find the dimensions of the rectangular garden in meters. Find the garden area in square meters. - Square metal sheet
 We cut out four squares of 300 mm side from a square sheet metal plate with a side of 0,7 m. Express the fraction and the percentage of waste from the square metal sheet.
We cut out four squares of 300 mm side from a square sheet metal plate with a side of 0,7 m. Express the fraction and the percentage of waste from the square metal sheet. - Hexagon ABCDEF
 In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area.
In the regular hexagon ABCDEF, the diagonal AE has a length of 8cm. Calculate the circumference and the hexagon area. - Right triangle eq2
 The hypotenuse of a right triangle is 9 cm longer than one leg and 8 cm longer than the second leg. Determine the circumference and area of a triangle.
The hypotenuse of a right triangle is 9 cm longer than one leg and 8 cm longer than the second leg. Determine the circumference and area of a triangle. - The field
 The player crossed the field diagonally and walked the length of 250 m. Calculate the length of the field circumference if one side of the field is 25 meters.
The player crossed the field diagonally and walked the length of 250 m. Calculate the length of the field circumference if one side of the field is 25 meters. - Chord 2
 Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle.
Point A has a distance of 13 cm from the circle's center with a radius r = 5 cm. Calculate the length of the chord connecting the points T1 and T2 of contact of tangents led from point A to the circle. - Arc and segment
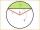 Calculate the length of circular arc l, area of the circular arc S1 and area of circular segment S2. The circle's radius is 11, and the corresponding angle is (2)/(12) π.
Calculate the length of circular arc l, area of the circular arc S1 and area of circular segment S2. The circle's radius is 11, and the corresponding angle is (2)/(12) π. - 13680m2 70374
 Eight painters painted an area of 15200 m² in 5 days. How many painters will paint a room of 13680 m² in 3 days?
Eight painters painted an area of 15200 m² in 5 days. How many painters will paint a room of 13680 m² in 3 days? - Circuits 17961
 The area of one square is 81 cm2, and the area of the other is 225 cm². What is the ratio of their circuits?
The area of one square is 81 cm2, and the area of the other is 225 cm². What is the ratio of their circuits? - The perimeter
 The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
The perimeter of a rhombus whose diagonal lengths are in the ratio 3:4 is 40 cm. What is its area in cm²?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
