Practice problems of the area of a right triangle
Number of problems found: 668
- A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Calculate 83265
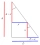 Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm.
Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm. - Calculate 83261
 Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 - Centimeters 83177
 The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up?
The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up? - Overhangs 83158
 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Determine 82724
 A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the content of this square.
A right triangle has an area of 36 cm². A square is placed in it so that two sides of the square are parts of two sides of a triangle, and one vertex of the square is in a third of the longest side. Determine the content of this square. - Construction 82703
 The plot of land for constructing family houses is shaped like a rectangular trapezoid with bases of 21m and 11.2m. For CZK 2,500 per square meter, the value of the land is calculated at CZK 1,352,400. What would be the length of wire mesh needed to fence
The plot of land for constructing family houses is shaped like a rectangular trapezoid with bases of 21m and 11.2m. For CZK 2,500 per square meter, the value of the land is calculated at CZK 1,352,400. What would be the length of wire mesh needed to fence - Calculate 82700
 A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume.
A cone of rotation with a radius of 32 cm and side length s = 65 cm is given. Calculate the surface area and volume. - Calculate 82690
 A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume.
A cone of rotation with a height of 18 cm and side length s = 45 cm is given. Calculate the surface area and volume. - Circle - analytics geometry
 Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0.
Write the equation of the circle that passes through the points Q[3.5] R[2.6] and has its center on the line 2x+3y-4=0. - Parallelogram 82626
 Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer.
Calculate the area of a parallelogram if we know the perimeter is 23 cm, the diagonal is 8.5 cm, and one side is 1.5 cm longer. - Equilateral 82576
 Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm.
Calculate the volume and surface area of a 9.6 cm high prism with a base of an equilateral triangle of length 4.8 cm. - ABCDEFGH 82499
 In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG?
In the cube ABCDEFGH, the area of triangle ABK is √20 cm². How much cm² is the volume of ABGH in a cube if you know that K is the midpoint of edge CG? - Calculate 82490
 Calculate the area of an isosceles triangle ABC with a base of 10 cm and a side of 7 cm. Sketch a picture.
Calculate the area of an isosceles triangle ABC with a base of 10 cm and a side of 7 cm. Sketch a picture. - Perpendicular 82473
 In the right triangle KLM, the hypotenuse l = 9 cm and the perpendicular k = 6 cm. Calculate the size of the height vl and the line tk.
In the right triangle KLM, the hypotenuse l = 9 cm and the perpendicular k = 6 cm. Calculate the size of the height vl and the line tk. - Right-angled 82471
 The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c
The lengths a = 7.2 cm and b = 10.4 cm are dropped in the right-angled triangle ABC. Do the math a) lengths of the sections of the hypotenuse b) height on the hypotenuse c
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
