Practice problems of the area of a triangle
Number of problems found: 899
- ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - The triangle 6
 The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning.
The triangle has an area of 7 ⅞ cm² and a base of 5 ¼ cm. What is the length of h? Explain your reasoning. - Panting
 If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.?
If the base of the triangle is 2 3/4 meters & and the altitude is 3 2/3 meters, then what is the cost of panting on both sides at ₹3 1/2 per sq.m.? - Januka
 Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then
Januka and her father were going to the tent. They found that their old tent was torn. Their mother suggested that they sew a tent whose walls would be made of 4 identical isosceles triangles. Their lower side is 2 m long, and the height is also 2 m. Then - A lamp
 A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum?
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - The apothem
 The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area.
The apothem of a regular hexagon is 5√3 inches. Find one of its sides and area. - One side 4
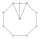 One side of a regular octagon is 12 inches. Find the apothem and its area.
One side of a regular octagon is 12 inches. Find the apothem and its area. - Area - simple
 Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area?
Find the area of the triangle. So, the base is 7 2/3 mi. The height is 7 mi. What is the Area? - Storage shed
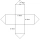 Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of
Frank designed a net for a storage shed that he is going to construct out of metal. The design consists of a square base and four square sides, plus four triangular parts that make up the roof. A square base of 6 feet and four square sides, plus 4 feet of - The volume 8
 The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height.
The volume of a right regular hexagonal prism is 187.2 cubic millimeters. The line segment that has a length of 2.6 millimeters begins at the center of the hexagon and ends at one side of the hexagon. 3 mm base. Find the height. - A triangle 9
 A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base?
A triangle has an area of 16 1/2 square units. The height is 3 2/3. What is the base? - A triangle 8
 A triangle has a base of 9.2 feet and a height of 4.8 feet. What is the area of the triangle?
A triangle has a base of 9.2 feet and a height of 4.8 feet. What is the area of the triangle? - Quadrilateral 83324
 The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid.
The volume of a regular quadrilateral pyramid is 72 cm³. Its height is equal to the length of the base edge. Calculate the length of the base and the surface of the pyramid. - Equilateral 83322
 The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³?
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Calculate 83265
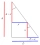 Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm.
Calculate the area of a right-angled triangle ABC with a=15 cm, b=1.7 dm. - Calculate 83261
 Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3
Calculate the area of the triangle ABC, in which you know the side c=5 cm, the angle at the top A= 70 degrees, and the ratio of the segments cut by the height to the side c is 1:3 - Perimeter 83259
 The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area.
The perimeter of the four-sided needle is 48 m, and its height is 2.5 m; how much will the sheet metal for this pyramid cost? If 1m² costs €1.5, a 12% loss due to joints and folds is included in the area. - Centimeters 83177
 The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up?
The carpenter cut a right-angled triangle with free sides of 550 mm and 200 mm from the wooden canvas, the face of a rectangle with dimensions of 80 CM and 65 CM. How many square centimeters will the waste make up? - Overhangs 83158
 The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b.
The area of a right triangle ABC is 346 cm2, and the angle at vertex A is 64°. Calculate the lengths of the overhangs a and b. - Circumscribed 83152
 Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle.
Given is an isosceles triangle whose base is 8 cm, and the sides are 15 cm long. Calculate the area of the triangle and the radius of the inscribed and circumscribed circle.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
