Practice problems of the area of a trapezoid - page 4 of 9
Number of problems found: 174
- Transplants 29961
 In the middle of the square, they created a flower bed in the shape of an isosceles trapezoid. The parallel sides are 12 m and 8 m long. The bed is 6 m wide. How many flower transplants do they need to plant a flower bed if 4 dm² of space must be counted
In the middle of the square, they created a flower bed in the shape of an isosceles trapezoid. The parallel sides are 12 m and 8 m long. The bed is 6 m wide. How many flower transplants do they need to plant a flower bed if 4 dm² of space must be counted - Truncated pyramid
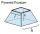 The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Dimensions of the trapezoid
 One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2
One of the trapezoid bases is one-fifth larger than its height, and the second base is 1 cm larger than its height. Find the dimensions of the trapezoid if its area is 115 cm2 - Four prisms
 Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t
Question No. 1: The prism has the dimensions a = 2.5 cm, b = 100 mm, c = 12 cm. What is its volume? a) 3000 cm² b) 300 cm² c) 3000 cm³ d) 300 cm³ Question No.2: The prism base is a rhombus with a side length of 30 cm and a height of 27 cm. The height of t
- Isosceles 27793
 The LICH isosceles trapezoid has 5.2 cm long arms and its bases are 7.6 cm and 3.6 cm long. Find the area of the LICH trapezoid.
The LICH isosceles trapezoid has 5.2 cm long arms and its bases are 7.6 cm and 3.6 cm long. Find the area of the LICH trapezoid. - The trench
 Calculate how many cubic meters of soil needs to be removed from the excavation in the shape of an isosceles trapezoid. The top width is 3 meters, the lower width is 1.8 m, the excavation depth is 1 m, and the length is 20 m.
Calculate how many cubic meters of soil needs to be removed from the excavation in the shape of an isosceles trapezoid. The top width is 3 meters, the lower width is 1.8 m, the excavation depth is 1 m, and the length is 20 m. - Quadrilateral 24161
 Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated?
Calculate the volume of a quadrilateral prism whose base is an isosceles trapezoid with bases 10 cm and 4 cm, 6 cm apart. The height of the prism is 25 cm. How could the surface area be calculated? - Cross-section 23491
 The cross-section of the railway embankment is an isosceles trapezoid, the bases of which are in a ratio of 5:3. The arms have a 5 m embankment height v = 4.8 m. Calculate the section area S.
The cross-section of the railway embankment is an isosceles trapezoid, the bases of which are in a ratio of 5:3. The arms have a 5 m embankment height v = 4.8 m. Calculate the section area S. - The bases
 The bases of the isosceles trapezoid ABCD have 10 cm and 6 cm lengths. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and area of the ABCD trapezoid.
The bases of the isosceles trapezoid ABCD have 10 cm and 6 cm lengths. Its arms form an angle α = 50˚ with a longer base. Calculate the circumference and area of the ABCD trapezoid.
- Garden exchange
 The garden has a rectangular trapezoid shape, the bases of which have dimensions of 60 m and 30 m and a vertical arm of 40 m. The owner exchanged this garden for a parallelogram, which is 7/9 of the area of a trapezoidal garden. What is the size of the ne
The garden has a rectangular trapezoid shape, the bases of which have dimensions of 60 m and 30 m and a vertical arm of 40 m. The owner exchanged this garden for a parallelogram, which is 7/9 of the area of a trapezoidal garden. What is the size of the ne - Calculate 20643
 Calculate the area and perimeter of the building plot in the shape of an isosceles trapezoid with a base of 120 m, 95 m, and a height of 50 m.
Calculate the area and perimeter of the building plot in the shape of an isosceles trapezoid with a base of 120 m, 95 m, and a height of 50 m. - Horses playground
 The fence for the horses has the shape of a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. How many meters of boards will they need to fence if they are stacked in 5 rows?
The fence for the horses has the shape of a rectangular trapezoid with an area of 400 m². The base lengths should be 31 m and 19 m. How many meters of boards will they need to fence if they are stacked in 5 rows? - Rectangular 18993
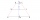 The bases are 9 cm and 50 mm long in a rectangular trapezoid. The length of the shorter arm is 3 cm. Calculate the circuit and area.
The bases are 9 cm and 50 mm long in a rectangular trapezoid. The length of the shorter arm is 3 cm. Calculate the circuit and area. - Cross-sectional 18973
 Calculate the cross-sectional area of the trapezoidal channel irrigation channel if its upper width is 7.9 m, its bottom width is 5.5 m, and its depth is 2.8 m.
Calculate the cross-sectional area of the trapezoidal channel irrigation channel if its upper width is 7.9 m, its bottom width is 5.5 m, and its depth is 2.8 m.
- Dimensions 18833
 The 4-sided prism has a volume of 648 cubic cm. The trapezoid, its base, has the dimensions a-10cm, c-8cm, h-6cm. Calculate the height of the prism
The 4-sided prism has a volume of 648 cubic cm. The trapezoid, its base, has the dimensions a-10cm, c-8cm, h-6cm. Calculate the height of the prism - Trapezoid 18313
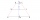 Find the points A1 B1 symmetric along the y-axis to the points A [-4,0], B [-1,4]. Calculate the perimeter of the trapezoid AB B1 A1.
Find the points A1 B1 symmetric along the y-axis to the points A [-4,0], B [-1,4]. Calculate the perimeter of the trapezoid AB B1 A1. - Cross-section 17871
 The road embankment has a cross-section of an isosceles trapezoid with bases 16 m and 10 m long and with arms 5 m long. How many cubic meters of soil is in the 400 m long dam?
The road embankment has a cross-section of an isosceles trapezoid with bases 16 m and 10 m long and with arms 5 m long. How many cubic meters of soil is in the 400 m long dam? - Trapezoid 16783
 The garden, in the shape of an isosceles trapezoid, has a base length of 44 m and 16 meters. The arms are 25 m long. 1/5 of the area is for a road and a cottage. How many m² of the area will be left for planting trees?
The garden, in the shape of an isosceles trapezoid, has a base length of 44 m and 16 meters. The arms are 25 m long. 1/5 of the area is for a road and a cottage. How many m² of the area will be left for planting trees? - Diagonal intersect
 Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Isosceles trapezoid ABCD with length bases | AB | = 6 cm, CD | = 4 cm is divided into four triangles by the diagonals intersecting at point S. How much of the area of the trapezoid are ABS and CDS triangles?
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
