Circle + Pythagorean theorem - practice problems
Number of problems found: 226
- Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - Radio radius
 Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both
Two friends have shortwave radios with a range of 13 km. The first of them travels by train at a speed of 48 km per hour along a straight section of track, from which the second of the friends is 5 km away. How long will radio friends be allowed for both - MO circles
 Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Diameter
 If the endpoints of the diameter of a circle are A(-9, 10) and B (-5, -4), what is the circle's radius?
If the endpoints of the diameter of a circle are A(-9, 10) and B (-5, -4), what is the circle's radius? - Equation of circle
 Find an equation of the circle with indicated properties: a. center at (-3,5), diameter 20. b. center at origin and diameter 16.
Find an equation of the circle with indicated properties: a. center at (-3,5), diameter 20. b. center at origin and diameter 16. - Equation of the circle
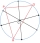 Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2).
Find an equation of the circle whose diameter has endpoints (1,-4) and (3,2). - Round table
 A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners?
A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners? - Calculate 39131
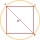 A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square.
A circle describes a square with a side of 8 cm. Calculate the area of the rest of the circle if we cut out the square. - Equilateral triangle vs circle
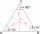 Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy?
Find the area of an equilateral triangle inscribed in a circle of radius r = 9 cm. What percentage of the circle area does it occupy? - Circle inscribed
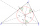 There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26?
There is a triangle ABC and a circle inscribed in this triangle with a radius of 15. Point T is the point of contact of the inscribed circle with the side BC. What is the area of the triangle ABC if | BT | = 25 a | TC | = 26? - RT sides
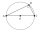 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Semicircle
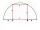 To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides?
To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides? - Logs
 The log has a diameter of 30 cm. What largest beam with a rectangular cross-section can carve from it?
The log has a diameter of 30 cm. What largest beam with a rectangular cross-section can carve from it? - Tree trunk
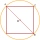 What is the smallest diameter of a tree trunk that we can cut a square-section square with a side length of 20 cm?
What is the smallest diameter of a tree trunk that we can cut a square-section square with a side length of 20 cm? - Circumference 4278
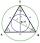 An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle?
An inscribed circle is also described as an equilateral triangle with a side length of 8 cm. How many cm is the circumference of the inscribed circle smaller than the circumference of the described circle? - Right triangle
 A circle with a radius of 5 cm is described in a right triangle with a 6 cm leg. What is the height at the hypotenuse of this triangle?
A circle with a radius of 5 cm is described in a right triangle with a 6 cm leg. What is the height at the hypotenuse of this triangle? - EQL triangle
 Calculate the inradius and circumradius of an equilateral triangle with side a=77 cm.
Calculate the inradius and circumradius of an equilateral triangle with side a=77 cm. - Circumscribed 3132
 The right triangle has squares in the ratio of 5:12, and the circumscribed circle diameter is 26 cm. Determine its perimeter.
The right triangle has squares in the ratio of 5:12, and the circumscribed circle diameter is 26 cm. Determine its perimeter.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
