Circle + square (second power, quadratic) - practice problems
Number of problems found: 264
- Pizza diameter
 If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch?
If an 18-inch pizza costs $16.99 and is cut into 12 slices, what is the cost per square inch? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - A cone 3
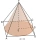 A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain.
A cone has a diameter of x cm and a slant height of y cm. A square pyramid has a base side length of x cm and a slant height of y cm. Which has the greater surface area? Explain. - The length 17
 The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord.
The length of one of two chords of a circle is 12cm. If the chords are 6cm and 7cm, respectively, away from the center of the circle, calculate the length of the second chord. - A goat 2
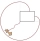 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - Circumferential 2367
 Recently, two spacecraft successfully landed on two small planets labeled α and β. Both ships were equipped with sensitive sensors that measured the basic parameters of the asteroids. The sensors found that the day α took six times longer on planet α than
Recently, two spacecraft successfully landed on two small planets labeled α and β. Both ships were equipped with sensitive sensors that measured the basic parameters of the asteroids. The sensors found that the day α took six times longer on planet α than - Two gears
 The gearbox will use a large gear to turn a smaller gear. The large gear will make 75 revolutions per minute, while the smaller gear must make 384 revolutions per minute. Find the smallest number of teeth each gear could have. [Hint: Use either GCF or LCM
The gearbox will use a large gear to turn a smaller gear. The large gear will make 75 revolutions per minute, while the smaller gear must make 384 revolutions per minute. Find the smallest number of teeth each gear could have. [Hint: Use either GCF or LCM - Approximately 20243
 Lake Trasimeno is approximately in the shape of a circle, its area is about 28 square kilometers, and Mr. Hector's walking speed is approximately 4km/h. Calculate the length of the path around the lake and how many hours Mr. Hector would have to walk to o
Lake Trasimeno is approximately in the shape of a circle, its area is about 28 square kilometers, and Mr. Hector's walking speed is approximately 4km/h. Calculate the length of the path around the lake and how many hours Mr. Hector would have to walk to o - MO circles
 Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th
Juro built the ABCD square with a 12 cm side. In this square, he scattered a quarter circle with a center at point B passing through point A and a semicircle l with a center at the center of the BC side and passed point B. He would still build a circle th - Centimeters 6220
 A pizza in the shape of a circle occupies an area of 94.985 square cm. What is the smallest integer diameter in centimeters that the plate on which we want to place this pizza must have so that the plates do not overlap
A pizza in the shape of a circle occupies an area of 94.985 square cm. What is the smallest integer diameter in centimeters that the plate on which we want to place this pizza must have so that the plates do not overlap - Calculated 4765
 The volume of the cylinder is calculated as V = 1/4 pi times d on the type times v. Express the average d using the volume V and the height in the cylinder. Calculate d for V = 1000 l and v = 23dm
The volume of the cylinder is calculated as V = 1/4 pi times d on the type times v. Express the average d using the volume V and the height in the cylinder. Calculate d for V = 1000 l and v = 23dm - Wiring
 The conduit has a cross-section 54² mm. Maybe put it into 6 conductors with a cross section S2 $mm²?
The conduit has a cross-section 54² mm. Maybe put it into 6 conductors with a cross section S2 $mm²? - Four circles
 1) Calculate the circle radius if its area is 400 cm square 2) Calculate the radius of the circle whose circumference is 400 cm. 3) Calculate circle circumference if its area is 400 cm square 4) Calculate the circle's area if the perimeter is 400 cm.
1) Calculate the circle radius if its area is 400 cm square 2) Calculate the radius of the circle whose circumference is 400 cm. 3) Calculate circle circumference if its area is 400 cm square 4) Calculate the circle's area if the perimeter is 400 cm. - Approximately 17143
 The decorative round flowerbed has a diameter of 480 cm. How many tulips can we plant in the flowerbed when we count approximately 25 cm of square land per 1 tulip?
The decorative round flowerbed has a diameter of 480 cm. How many tulips can we plant in the flowerbed when we count approximately 25 cm of square land per 1 tulip? - Round table
 A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners?
A round table with a diameter d = 105 cm is coated by a square tablecloth with a side length 121 cm. About how many cm is the higher center of the tablecloth than its corners? - Percentage 3980
 Calculate the percentage of waste when we cut out 4 of the largest possible circles from a square sheet with sides of 1 meter.
Calculate the percentage of waste when we cut out 4 of the largest possible circles from a square sheet with sides of 1 meter. - Circumference 40401
 Calculate the diameter of a circle whose area in cm² and the circumference in cm are expressed by the same number.
Calculate the diameter of a circle whose area in cm² and the circumference in cm are expressed by the same number. - Integer 7814
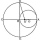 The small circle in the picture has an area of 3.5 cm². It touches from the inside and passes through the center of the large circle. What is the area of a large circle? The result round to an integer.
The small circle in the picture has an area of 3.5 cm². It touches from the inside and passes through the center of the large circle. What is the area of a large circle? The result round to an integer. - Cutting circles
 From the square 1 m sides, we have to cut the circles with a radius of 10 cm. How many discs will we cut, and how many percent will be wasted?
From the square 1 m sides, we have to cut the circles with a radius of 10 cm. How many discs will we cut, and how many percent will be wasted? - Circumference 20933
 Calculates the circumference of a circle if its area is S = 2119.5 cm².
Calculates the circumference of a circle if its area is S = 2119.5 cm².
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
