Circle + quadratic equation - practice problems
Number of problems found: 45
- Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Circumference 40401
 Calculate the diameter of a circle whose area in cm² and the circumference in cm are expressed by the same number.
Calculate the diameter of a circle whose area in cm² and the circumference in cm are expressed by the same number. - RT sides
 Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm.
Find the sides of a rectangular triangle if legs a + b = 17cm and the radius of the written circle ρ = 2cm. - Semicircle
 To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides?
To a semicircle with a diameter of 10 cm, inscribe a square. What is the length of the square sides?
- Radius
 Find the radius of the circle with area S = 200 cm².
Find the radius of the circle with area S = 200 cm². - Right-angled triangle
 Determine the area of a right triangle whose side lengths form successive members of an arithmetic progression, and the radius of the circle described by the triangle is 5 cm.
Determine the area of a right triangle whose side lengths form successive members of an arithmetic progression, and the radius of the circle described by the triangle is 5 cm. - Find radius
 Find the radius of the circle using the Pythagorean theorem where a=9, b=r, c= 6+r
Find the radius of the circle using the Pythagorean theorem where a=9, b=r, c= 6+r - RT and circles
 Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=23.
Solve the right triangle if the radius of the inscribed circle is r=9 and the radius of the circumscribed circle is R=23. - Quatrefoil 81138
 Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters.
Gothic quatrefoil is an ornament in which four identical touching smaller circles are inscribed in a larger circle, as you can see in the picture. The radius of the great circle is one meter. Calculate the radius of the smaller circle in meters.
- Woman's day
 We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1?
We can easily make a heart for mothers for Woman's day by drawing two semicircles on the two upper sides of the square standing on their top. What is the radius of the circle circumscribed by this heart when the length of the side of the square is 1? - Circle
 Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r²
Write the equation of a circle that passes through the point [0,6] and touches the X-axis point [5,0]: (x-x_S)²+(y-y_S)²=r² - Touch x-axis
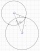 Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis.
Find the equations of circles that pass through points A (-2; 4) and B (0; 2) and touch the x-axis. - Intersections 3
 Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0 - Tangents
 To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center.
To circle with a radius of 41 cm from the point R guided two tangents. The distance of both points of contact is 16 cm. Calculate the distance from point R and circle center.
- Circle and square
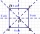 An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD.
An ABCD square with a side length of 100 mm is given. Calculate the circle’s radius that passes through vertices B, C, and the center of the side AD. - Circle
 From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r.
From the equation of a circle: -x² -y² +16x -4y -59 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and the radius of the circle r. - Flowerbed
 We enlarged the circular flower bed, so its radius increased by 3 m. The substrate consumption per enlarged flower bed was (at the same layer height as before magnification) nine times greater than before. Determine the original flowerbed radius.
We enlarged the circular flower bed, so its radius increased by 3 m. The substrate consumption per enlarged flower bed was (at the same layer height as before magnification) nine times greater than before. Determine the original flowerbed radius. - A circle
 A circle relation is given to be x² + y² =16. What is the radius of the circle?
A circle relation is given to be x² + y² =16. What is the radius of the circle? - Ratio of sides
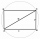 Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Calculate the area of a circle with the same circumference as the circumference of the rectangle inscribed with a circle with a radius of r 9 cm so that its sides are in a ratio of 2 to 7.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
