Cuboid + area - practice problems - page 5 of 16
Number of problems found: 302
- Dimensions 26401
 How many square meters of wallpaper will we need to cover the walls of a room with dimensions of 3 m and 4 m if the room height is 2.5 m? A door with dimensions of 90 cm and 2 m leads to the room. There is one window 1 m wide and 1.5 m high.
How many square meters of wallpaper will we need to cover the walls of a room with dimensions of 3 m and 4 m if the room height is 2.5 m? A door with dimensions of 90 cm and 2 m leads to the room. There is one window 1 m wide and 1.5 m high. - Dimensions 3985
 The block of goods has dimensions of 2.5 m, 4.2 m, and a height of 180 cm. It is filled to two-thirds of the volume. How much is hl of water in it? How many m² of the tank is soaked with water?
The block of goods has dimensions of 2.5 m, 4.2 m, and a height of 180 cm. It is filled to two-thirds of the volume. How much is hl of water in it? How many m² of the tank is soaked with water? - Dimensions 2717
 We will paint a block-shaped pool with 25m and 15m bottom dimensions and a depth of 3.5m. How much € will we pay for painting if we paint twice? One kilogram of paint is enough for 5m² of paint; we will pay €3.5 for 1kg of paint, and we have to pay the pa
We will paint a block-shaped pool with 25m and 15m bottom dimensions and a depth of 3.5m. How much € will we pay for painting if we paint twice? One kilogram of paint is enough for 5m² of paint; we will pay €3.5 for 1kg of paint, and we have to pay the pa - How many
 How many cans of blue paint need to be bought if the interior of the garden pool, which is 5 m long, 3 m wide, and 1 m deep, is to be painted? There is 1 kg of paint in each can. One can is enough for 8 m² of area.
How many cans of blue paint need to be bought if the interior of the garden pool, which is 5 m long, 3 m wide, and 1 m deep, is to be painted? There is 1 kg of paint in each can. One can is enough for 8 m² of area. - Dimensions 16813
 Calculate how many bricks we will need to build a room that should be 1.8 m wide, 2 m long, and 2.4 m high. The dimensions of the brick are 25 cm x 60 cm.
Calculate how many bricks we will need to build a room that should be 1.8 m wide, 2 m long, and 2.4 m high. The dimensions of the brick are 25 cm x 60 cm. - Two-thirds 3388
 The kneaded cake dough has a volume of 1.8 l. When baking, it increases its volume by about two-thirds. Can a baked wheel fit on a baking sheet measuring 36x30x8cm? How tall will the cake be after baking?
The kneaded cake dough has a volume of 1.8 l. When baking, it increases its volume by about two-thirds. Can a baked wheel fit on a baking sheet measuring 36x30x8cm? How tall will the cake be after baking? - Dimensions 16493
 How many square meters of material is needed to make two identical blocks with dimensions of 6 dm, 8 dm, and 12 dm if we count 8% of the material for folds? (Round to two decimal places. )
How many square meters of material is needed to make two identical blocks with dimensions of 6 dm, 8 dm, and 12 dm if we count 8% of the material for folds? (Round to two decimal places. ) - The pool
 The pool is 25 meters long, 10 meters wide, and 1.5 meters deep. How many liters are needed to fill it completely? How much will the new floor and wall paneling cost if one m² costs 10 euros?
The pool is 25 meters long, 10 meters wide, and 1.5 meters deep. How many liters are needed to fill it completely? How much will the new floor and wall paneling cost if one m² costs 10 euros? - Wooden box
 The block-shaped box was placed on the ground, leaving a rectangular print with 3 m and 2 m. When flipped over to another wall, a print with dimensions of 0.5 m and 3 m remained in the sand. What is the volume of the wooden box?
The block-shaped box was placed on the ground, leaving a rectangular print with 3 m and 2 m. When flipped over to another wall, a print with dimensions of 0.5 m and 3 m remained in the sand. What is the volume of the wooden box? - Length 25661
 How many liters of water are in a pool whose width is 12 m, length 25 m, and depth 280 cm if it is filled 10 cm below the edge? What area of the walls wet the water (in m2)?
How many liters of water are in a pool whose width is 12 m, length 25 m, and depth 280 cm if it is filled 10 cm below the edge? What area of the walls wet the water (in m2)? - Bathroom
 How much CZK do we pay for lining the perimeter walls of the bathroom with rectangular shapes with dimensions of 3.5 m and 4 m, high 1.5 m if 1 square m tile costs 300 CZK?
How much CZK do we pay for lining the perimeter walls of the bathroom with rectangular shapes with dimensions of 3.5 m and 4 m, high 1.5 m if 1 square m tile costs 300 CZK? - Block-shaped 31741
 We will paint the block-shaped pool, with the dimensions of the bottom a = 25 m and b = 15 m and the height c = 3.5 m. If one kg is enough for five square meters of paint, how many kg of paint will we need?
We will paint the block-shaped pool, with the dimensions of the bottom a = 25 m and b = 15 m and the height c = 3.5 m. If one kg is enough for five square meters of paint, how many kg of paint will we need? - Centimeters 6989
 The pool measures 4 m and 3 m, and 2.5 m. What height does the water in the pool reach if 25 m³ of water has been added? Round the result to centimeters.
The pool measures 4 m and 3 m, and 2.5 m. What height does the water in the pool reach if 25 m³ of water has been added? Round the result to centimeters. - Calculate 4784
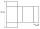 The sketch shows a network of blocks with a surface size of 150 cm². Calculate its volume. (MONITOR 9 - 2005/30 question.)
The sketch shows a network of blocks with a surface size of 150 cm². Calculate its volume. (MONITOR 9 - 2005/30 question.) - Dimensions 33763
 The pool has dimensions of 4.8 m and 65 dm. To what height is water filled in a pool if there is 1,029.6 hl of water in it?
The pool has dimensions of 4.8 m and 65 dm. To what height is water filled in a pool if there is 1,029.6 hl of water in it? - Rectangular 4546
 Thirty watering cans of 8 liters of water are brought to the rectangular garden measuring 15 m and 10 m. During the rain, 2 mm of water fell on the garden. When was the flowerbed more watered?
Thirty watering cans of 8 liters of water are brought to the rectangular garden measuring 15 m and 10 m. During the rain, 2 mm of water fell on the garden. When was the flowerbed more watered? - Bricks wall
 There are 5000 bricks. How high wall thicknesses of 20 cm around the area, which has dimensions of 20 m and 15 m, can use these bricks to build? Brick dimensions are 30 cm, 20 cm, and 10 cm.
There are 5000 bricks. How high wall thicknesses of 20 cm around the area, which has dimensions of 20 m and 15 m, can use these bricks to build? Brick dimensions are 30 cm, 20 cm, and 10 cm. - Dimensions 20553
 The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume.
The surface of the block is 558 cm², and its dimensions are in the ratio of 5:3:2. Calculate the volume. - Bottom 3129
 How many m² tiles do we need to line the walls and bottom of the pool in the shape of a block 25 m long, 10 m wide, and 180 cm deep?
How many m² tiles do we need to line the walls and bottom of the pool in the shape of a block 25 m long, 10 m wide, and 180 cm deep? - Ratio-cuboid
 The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
The lengths of the edges of the cuboid are in the ratio 2: 3: 6. Its body diagonal is 14 cm long. Calculate the volume and surface area of the cuboid.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
