Practice problems of the of a diagonal of a trapezoid
Number of problems found: 36
- Trapezoid
 Are diagonals in a rectangular trapezoid perpendicular and bisect the angles?
Are diagonals in a rectangular trapezoid perpendicular and bisect the angles? - Trapezoid - hard example
 Bases of the trapezoid are: 24, 16 cm. Diagonal 22, 26 cm. Calculate its area and perimeter.
Bases of the trapezoid are: 24, 16 cm. Diagonal 22, 26 cm. Calculate its area and perimeter. - Trapezoid and diagonals
 Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm.
Find the area of a trapezoid with bases a = 24 cm, c = 16 cm, and diagonals u = 22 cm, v = 26 cm. - The trapezium
 The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium.
The trapezium is formed by cutting the top of the right-angled isosceles triangle. The trapezium base is 10 cm, and the top is 5 cm. Find the area of the trapezium. - Trapezoid ABCD
 ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD.
ABDC is a trapezoid in which AB and CD are parallel sides measuring 6 and 9, respectively. Angles ABC and BCD are both right angles. Find the length of segment BD. - Calculate square 2556
 Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square.
Calculate the arm length b of the trapezoid ABCD if a = 12 cm, c = 4 cm, the length of AC is same as the length of BC and the area S of the triangle ABC is 9 cm square. - Rectangular trapezoid
 Calculate the area of a rectangular trapezoid with a right angle at point A and if |AC| = 4 cm, |BC| = 3 cm, and the diagonal AC is perpendicular to the side BC.
Calculate the area of a rectangular trapezoid with a right angle at point A and if |AC| = 4 cm, |BC| = 3 cm, and the diagonal AC is perpendicular to the side BC. - KLMN
 In the KLMN trapezoid is given this information: 1. segments KL and MN are parallel 2. segments KL and KM have the same length 3. segments KN, NM, and ML have the same length. Determine the size of the angle KMN.
In the KLMN trapezoid is given this information: 1. segments KL and MN are parallel 2. segments KL and KM have the same length 3. segments KN, NM, and ML have the same length. Determine the size of the angle KMN. - Consider 3
 Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid.
Consider the isosceles trapezoid PQRS. The bases are |PQ|=120 mm, |RS|=62 mm and the arm s=48 mm. Find the height of the trapezoid, diagonal length and the area of the trapezoid. - Diagonals 81884
 In an isosceles trapezoid, the basic lengths are 15 cm and 9 cm. The diagonals are 13 cm long. Calculate the perimeter and area of the trapezoid.
In an isosceles trapezoid, the basic lengths are 15 cm and 9 cm. The diagonals are 13 cm long. Calculate the perimeter and area of the trapezoid. - Right trapezoid
 The right trapezoid has bases 3.2 cm and 62 mm long. The shorter leg has a length of 0.25 dm. Calculate the lengths of the diagonals and the second leg.
The right trapezoid has bases 3.2 cm and 62 mm long. The shorter leg has a length of 0.25 dm. Calculate the lengths of the diagonals and the second leg. - Trapezoid - diagonal
 A trapezoid has a length of diagonal AC crossed with diagonal BD in the ratio of 2:1. The triangle created by points A, cross point of diagonals S, and point D has an area 164 cm². What is the area of the trapezoid?
A trapezoid has a length of diagonal AC crossed with diagonal BD in the ratio of 2:1. The triangle created by points A, cross point of diagonals S, and point D has an area 164 cm². What is the area of the trapezoid? - Diagonal BD
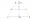 Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42°
Find the length of the diagonal BD in a rectangular trapezoid ABCD with a right angle at vertex A when/AD / = 8,1 cm and the angle DBA is 42° - Diagonal
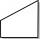 The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal.
The rectangular ABCD trapeze, whose AD arm is perpendicular to the AB and CD bases, has an area of 15 cm square. Bases have lengths AB = 6cm, CD = 4cm. Calculate the length of the AC diagonal. - IS trapezoid
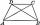 Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm.
Calculate the length of diagonal u and height v of isosceles trapezoid ABCD, whose bases have lengths a = |AB| = 37 cm, c = |CD| = 29 cm and legs b = d = |BC| = |AD| = 28 cm. - Trapezoid thirds
 The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment.
The ABCD trapezoid has parallel sides AB and CD. The E point lies on the AB side. The segment DE divides the trapezoid into two parts with the same area. Find the length of the AE line segment. - MO Z8–I–6 2018
 The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line.
The KLMN trapezium, KL has a 40 cm base and an MN of 16 cm. Point P lies on the KL line so that the NP segment divides the trapezoid into two parts with the same area. Find the length of the KP line. - Trapezoid 7537
 Diagonal alpha equals 0.4 m, and diagonal beta equals 0.4 m in the isosceles trapezoid. Side AB is 120 cm, and side DC is 7.6 dm. Find the length of arms in an isosceles trapezoid. Please result round to 2 decimal places.
Diagonal alpha equals 0.4 m, and diagonal beta equals 0.4 m in the isosceles trapezoid. Side AB is 120 cm, and side DC is 7.6 dm. Find the length of arms in an isosceles trapezoid. Please result round to 2 decimal places. - Trapezoid MO
 The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid.
The rectangular trapezoid ABCD with the right angle at point B, |AC| = 12, |CD| = 8, diagonals are perpendicular to each other. Calculate the perimeter and area of the trapezoid. - Inaccessible 69794
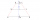 Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Determine the distance between two inaccessible places P, Q, if the distance between two observation points A, B is 2000m and if you know the size of the angles QAB = 52°40''; PBA = 42°01''; PAB = 86°40'' and QBA = 81°15''. The considered locations A, B,
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
