Division + reason - practice problems - page 2 of 11
Number of problems found: 211
- Opposite 79954
 We color a wooden cube with an edge length of 3 cm so that three walls are blue, three are red, and no two opposite walls are the same color. Cut the cube into 1 cm³ cubes. How many cats will have at least one red wall and at least one blue wall?
We color a wooden cube with an edge length of 3 cm so that three walls are blue, three are red, and no two opposite walls are the same color. Cut the cube into 1 cm³ cubes. How many cats will have at least one red wall and at least one blue wall? - Completely 79274
 Kitchen cabinets are sold in widths of 80 cm, 60 cm, and 40 cm. Which assembly can we choose if we have a wall 3.5 m long and we want to completely fill it with an assembly that also includes a dishwasher, the width of which is 60 cm, and the stove is 50
Kitchen cabinets are sold in widths of 80 cm, 60 cm, and 40 cm. Which assembly can we choose if we have a wall 3.5 m long and we want to completely fill it with an assembly that also includes a dishwasher, the width of which is 60 cm, and the stove is 50 - AMJ
 There are three siblings, Anne, Maya, and Jane. Anne gave Maya and Jane as much money as each had. Then Maya gave Anne and Jane as much money as each had. Then Jane gave Anne and Maya as much money as each had. Then each of the three had 128 pesos. How mu
There are three siblings, Anne, Maya, and Jane. Anne gave Maya and Jane as much money as each had. Then Maya gave Anne and Jane as much money as each had. Then Jane gave Anne and Maya as much money as each had. Then each of the three had 128 pesos. How mu - Polya's method
 On the way home from school, Dora likes to eat cookies. One daytime, just as she reached into her backpack, Swiper jumped into her path and grabbed her bag. It stole half of her cookies plus two more. A bit shaken, Dora continued home. Before she had a ca
On the way home from school, Dora likes to eat cookies. One daytime, just as she reached into her backpack, Swiper jumped into her path and grabbed her bag. It stole half of her cookies plus two more. A bit shaken, Dora continued home. Before she had a ca - Rectangles 70304
 How many rectangles with side lengths expressed in natural numbers have an area of 96 cm²?
How many rectangles with side lengths expressed in natural numbers have an area of 96 cm²? - Determine 69304
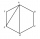 Determine the size of the ACF angle in the regular ABCDEF hexagon.
Determine the size of the ACF angle in the regular ABCDEF hexagon. - Prepared 66494
 Benches were prepared around the fire. When seven tourists sit on them, one tourist will sit alone on the last bench. When six of them all sat down, one had to stand. How many tourists were at the campfire if we know there were less than 100, and how many
Benches were prepared around the fire. When seven tourists sit on them, one tourist will sit alone on the last bench. When six of them all sat down, one had to stand. How many tourists were at the campfire if we know there were less than 100, and how many - Find two digits
 Find the possible values of A and B if the six-digit number 2A16B6 is divisible by 4 and 9. Please write the result as a composed number.
Find the possible values of A and B if the six-digit number 2A16B6 is divisible by 4 and 9. Please write the result as a composed number. - Proportion 65244
 Divide number 74 by 9, and find the proportion and the remainder. How much do we have to reduce the number 74 to halve the proportion and increase the remainder three times?
Divide number 74 by 9, and find the proportion and the remainder. How much do we have to reduce the number 74 to halve the proportion and increase the remainder three times? - Precisely 64114
 We painted a wooden cube with an edge 4 cm long with green paint over the entire surface. Then we cut it into small cubes with an edge length of 1 cm. The number of cubes that have precisely two faces colored green is:
We painted a wooden cube with an edge 4 cm long with green paint over the entire surface. Then we cut it into small cubes with an edge length of 1 cm. The number of cubes that have precisely two faces colored green is: - Dolls
 Dorotka cut the doll's way out of two batches. She was always left with one more doll, with every two dolls cut out. How many dolls did they cut in total if the number counted 16 of them in the first cut-out?
Dorotka cut the doll's way out of two batches. She was always left with one more doll, with every two dolls cut out. How many dolls did they cut in total if the number counted 16 of them in the first cut-out? - Expressions 62284
 Express the numbers 18, 28, 32, 40, 48, and 200 as numeric expressions composed of the digits 5.
Express the numbers 18, 28, 32, 40, 48, and 200 as numeric expressions composed of the digits 5. - Create 2
 Create word problems based on the given number sentence (300/24) - (207.60/24) = N
Create word problems based on the given number sentence (300/24) - (207.60/24) = N - How many
 How many double-digit numbers divided by nine give the rest of the seven?
How many double-digit numbers divided by nine give the rest of the seven? - Mr. Product
 The product of ages of all of Mr. Product's children is 1408. The age of the youngest child is equal to half the age of the oldest child. How many children does Mr. Product have, and how old are they?
The product of ages of all of Mr. Product's children is 1408. The age of the youngest child is equal to half the age of the oldest child. How many children does Mr. Product have, and how old are they? - Pechay
 Jan has 3/8 kilogram of pechay. If he shares 1/8 kilogram with each of his friends, how many of his friends can receive the pechay?
Jan has 3/8 kilogram of pechay. If he shares 1/8 kilogram with each of his friends, how many of his friends can receive the pechay? - Exchanged 59993
 Lukáš and Laco exchanged stamps. Before the exchange, Lukáš had 25 more marks than Laco. After the exchange, he had more Laco marks. At least how many stamps does Laco receive from Lukáš?
Lukáš and Laco exchanged stamps. Before the exchange, Lukáš had 25 more marks than Laco. After the exchange, he had more Laco marks. At least how many stamps does Laco receive from Lukáš? - Rectangular 56801
 We are to create a square in the shape of a rectangle with an area of 288 m² (square) so that the sides are whole numbers. What are all the dimensions of the rectangular box we can make? How many is the solution?
We are to create a square in the shape of a rectangle with an area of 288 m² (square) so that the sides are whole numbers. What are all the dimensions of the rectangular box we can make? How many is the solution? - Dividing
 One always remained when dividing the tangerines into packages of 8 or 10. How many were there, if more than 250 and less than 300?
One always remained when dividing the tangerines into packages of 8 or 10. How many were there, if more than 250 and less than 300? - Rajendra
 Rajendra, a farmer, had two sons and two daughters. He decided to divide his property among his sons and daughters. So he wrote a "WILL" about the distribution of his property. According to his "WILL," he desired to give 3/5 of the property to his sons in
Rajendra, a farmer, had two sons and two daughters. He decided to divide his property among his sons and daughters. So he wrote a "WILL" about the distribution of his property. According to his "WILL," he desired to give 3/5 of the property to his sons in
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
