Equation + sets - practice problems
Number of problems found: 41
- X intercept
 Given: 3y+2x=-6 Calculate the X-intercept.
Given: 3y+2x=-6 Calculate the X-intercept. - Find all 2
 Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8|
Find all the complex solutions (write the answer in the form x+iy) of the system. {|z-12|/|z-8i|=5/3 ; |z-4|=|z-8| - Determine 83003
 Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common.
Determine the value of the number a so that the graphs of the functions f: y = x² and g: y = 2x + a have exactly one point in common. - Parametrically 82990
 Calculate the sum of the x-coordinates of the intersections of the circle given by the equation (x - 1)²+ y² = 1 and the line given parametrically x = t, y = t , where t∈R.
Calculate the sum of the x-coordinates of the intersections of the circle given by the equation (x - 1)²+ y² = 1 and the line given parametrically x = t, y = t , where t∈R. - Children 82574
 Twenty-nine children attend the club. Eleven said that they have a dog, 14 children have a cat, and 12 children have a hamster. Two children have all three animals. Seven children do not have any animals at home. How many children have at least two of the
Twenty-nine children attend the club. Eleven said that they have a dog, 14 children have a cat, and 12 children have a hamster. Two children have all three animals. Seven children do not have any animals at home. How many children have at least two of the - Intersection 81611
 Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides.
Given a triangle ABC: A (-1,3), B(2,-2), C(-4,-3). Determine the coordinates of the intersection of the heights and the coordinates of the intersection of the axes of the sides. - Respondents 81024
 Out of 32 people, 22 like fish. Four fewer people will enjoy the mushrooms. Those who eat mushrooms or fish are 7 times more than those who do not eat mushrooms or fish. How many of the respondents have fish and mushrooms?
Out of 32 people, 22 like fish. Four fewer people will enjoy the mushrooms. Those who eat mushrooms or fish are 7 times more than those who do not eat mushrooms or fish. How many of the respondents have fish and mushrooms? - Intersections 80587
 Draw the graph of the function y = -2x + 3. Calculate the coordinates of the intersections of the function's graph with the x and y axes.
Draw the graph of the function y = -2x + 3. Calculate the coordinates of the intersections of the function's graph with the x and y axes. - A shopkeeper 5
 A shopkeeper sold some sets of Pencils and Pens. Each set contained 6 pencils and 2 pens. If the shopkeeper sold 112 pencils and pens, how many pens did she sell altogether?
A shopkeeper sold some sets of Pencils and Pens. Each set contained 6 pencils and 2 pens. If the shopkeeper sold 112 pencils and pens, how many pens did she sell altogether? - Positive integer integral
 How many different sets of a positive integer in the form (x, y, z) satisfy the equation xyz=1400?
How many different sets of a positive integer in the form (x, y, z) satisfy the equation xyz=1400? - Eighty-two 80493
 The sports club has 302 members. Ten times more members play soccer than tennis. Just one of the sports (F and T) is played by 222 members. Eighty-two members do not play football. How many members of the club play football? How many members play tennis?
The sports club has 302 members. Ten times more members play soccer than tennis. Just one of the sports (F and T) is played by 222 members. Eighty-two members do not play football. How many members of the club play football? How many members play tennis? - Intersection of Q2 with line
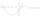 The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the
The equation of a curve C is y=2x² - 8x +9, and the equation of a line L is x + y=3. (1) Find the x-coordinates of the points of intersection of L and C. (ii) show that one of these points is also the - What is 19
 What is the equation of the line whose x-intercept is - 3 and y-intercept is -4? Find coefficients A, B, C in normal line equation: Ax + By = C
What is the equation of the line whose x-intercept is - 3 and y-intercept is -4? Find coefficients A, B, C in normal line equation: Ax + By = C - Children 58031
 The children talked about how they spent the holidays at school. 2/3 of them were on holiday with their parents. There were ten children by the sea, which is 5/8 of those who were on vacation. How many children are in the class of children?
The children talked about how they spent the holidays at school. 2/3 of them were on holiday with their parents. There were ten children by the sea, which is 5/8 of those who were on vacation. How many children are in the class of children? - Intersection 49623
 Where is the intersection of the function y = -3x + 5 with the coordinate axes x and y? (where they are on the x-axis and y-axis)
Where is the intersection of the function y = -3x + 5 with the coordinate axes x and y? (where they are on the x-axis and y-axis) - 25 pupils
 Twenty-five pupils attend the school dance group, which is 5 percent of all pupils. The judo class is attended by 20 pupils, a quarter of whom also go to a dance group. How many schoolchildren do not go to a dance or judo group?
Twenty-five pupils attend the school dance group, which is 5 percent of all pupils. The judo class is attended by 20 pupils, a quarter of whom also go to a dance group. How many schoolchildren do not go to a dance or judo group? - Please
 Please determine the solvability conditions of the equation, solve the equation and perform the test: x divided by x squared minus 2x plus1 the whole minus x + 3 divided by x squared minus one is equal to 0: x/(x²-2x+1) - (x+3)/( x²-1) = 0
Please determine the solvability conditions of the equation, solve the equation and perform the test: x divided by x squared minus 2x plus1 the whole minus x + 3 divided by x squared minus one is equal to 0: x/(x²-2x+1) - (x+3)/( x²-1) = 0 - Inequality: 33371
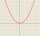 Solve the quadratic inequality: -2x² + 4x + 6
Solve the quadratic inequality: -2x² + 4x + 6 - Intersections 3
 Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0
Find the intersections of the circles x² + y² + 6 x - 10 y + 9 = 0 and x² + y² + 18 x + 4 y + 21 = 0 - Christmas or Easter
 Please calculate this example by the Venn equation. They asked 73 students whether they liked Christmas or Easter. Thirty-four of them like one of the holidays. 39 loves Easter. There are twice as many students who wish for both holidays as those who only
Please calculate this example by the Venn equation. They asked 73 students whether they liked Christmas or Easter. Thirty-four of them like one of the holidays. 39 loves Easter. There are twice as many students who wish for both holidays as those who only
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
