Exponentiation + square root - practice problems
Number of problems found: 58
- Perfect square or cube
 Would you classify 324 as a perfect square, perfect cube, both, or neither? ...
Would you classify 324 as a perfect square, perfect cube, both, or neither? ... - Evaluate 26
 Evaluate square root: √1³+2³+3³+4³=
Evaluate square root: √1³+2³+3³+4³= - Finite geometric sequence
 Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =?
Find the remaining unknown characteristics in the finite geometric sequence, if given: a1 = 18, an = 13122, sn = 19674, n =? q =? - Seventh term
 The first term of a geometric sequence is nine, and the third term is 1296. Find the seventh term.
The first term of a geometric sequence is nine, and the third term is 1296. Find the seventh term. - Equation 46771
 Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers
Insert three numbers between the roots of the equation 4x² - 17x + 4 = 0 so that they form with the given GP numbers - Annual increase
 The number of cars produced increased from 45,000 to 47,000 in 3 years. Calculate the average annual increase in cars in%.
The number of cars produced increased from 45,000 to 47,000 in 3 years. Calculate the average annual increase in cars in%. - Statistical 36383
 On the pages of the Czech Statistical Office, we can learn that in 1869, Prague and its suburbs had a total of 10,947 houses; in 1900, there were 18,838 houses. What was the annual percentage "increase" of houses in Prague between 1869 and 1900, assuming
On the pages of the Czech Statistical Office, we can learn that in 1869, Prague and its suburbs had a total of 10,947 houses; in 1900, there were 18,838 houses. What was the annual percentage "increase" of houses in Prague between 1869 and 1900, assuming - Percentage increase
 What is the annual percentage increase in the city when the population has tripled in 20 years?
What is the annual percentage increase in the city when the population has tripled in 20 years? - Original 18203
 There is a cube with an edge. How long must the cube's edge be in which the volume should be twice the volume of the original cube?
There is a cube with an edge. How long must the cube's edge be in which the volume should be twice the volume of the original cube? - Volume of wood
 Every year, at the same time, an increase in the volume of wood in the forest is measured. The increase is regularly p% compared to the previous year. If in 10 years the volume of wood has increased by 10%, what is the number p?
Every year, at the same time, an increase in the volume of wood in the forest is measured. The increase is regularly p% compared to the previous year. If in 10 years the volume of wood has increased by 10%, what is the number p? - A rectangle 2
 A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths.
A rectangle has a diagonal length of 74cm. Its side lengths are in a ratio of 5:3. Find its side lengths. - The tickets
 The tickets to the show cost some integer number greater than 1. Also, the sum of the price of the children's and adult tickets and their products was the power of the prime number. Find all possible ticket prices.
The tickets to the show cost some integer number greater than 1. Also, the sum of the price of the children's and adult tickets and their products was the power of the prime number. Find all possible ticket prices. - Six speeds
 A drilling machine is to have six speeds ranging from 50 to 750 revolutions per minute. If the speed forms a geometric progression, determine their values.
A drilling machine is to have six speeds ranging from 50 to 750 revolutions per minute. If the speed forms a geometric progression, determine their values. - Three members GP
 The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers.
The sum of three numbers in GP (geometric progression) is 21, and the sum of their squares is 189. Find the numbers. - Profit growth
 A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods.
A company's profit increased by 25% during 1992, increased by 40% during 1993, decreased by 20% in 1994, and increased by 10% during 1995. Find the average growth in the profit level over the four years periods. - Cube surface and volume
 Find the surface of the cube with a volume of 27 dm³.
Find the surface of the cube with a volume of 27 dm³. - Deposited 6059
 On January 2nd, 2009, Janko's father deposited €3,000 in the bank's passbook. The bank provides an annual interest of 0.30% for deposits up to €5,000. However, Janko's father collected the money after eight months. What is interest in euros added to it?
On January 2nd, 2009, Janko's father deposited €3,000 in the bank's passbook. The bank provides an annual interest of 0.30% for deposits up to €5,000. However, Janko's father collected the money after eight months. What is interest in euros added to it? - Determine 3888
 Determine the sum of the three-third roots of the number 64.
Determine the sum of the three-third roots of the number 64. - Fifth 3871
 What is the sum of the fifth root of 243?
What is the sum of the fifth root of 243? - Expression: 3865
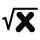 What is the value of this expression: (0.640.5): 4
What is the value of this expression: (0.640.5): 4
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
