Expression of a variable from the formula + frustum - practice problems
Number of problems found: 23
- Determine 73454
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Deviation 70434
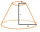Express the surface and volume of the cut cone using its side s if the following applies to the radii of the figures r1 and r2: r1> r2, r2 = s, and if the deviation of the side from the plane of the base is 60 °. - Frustrum - volume, area
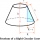Calculate the surface and volume of the truncated cone, the radius of the smaller figure is 4 cm, the height of the cone is 4 cm and the side of the truncated cone is 5 cm. - Top-open tank
The top-open tank has the shape of a truncated rotating cone, which stands on a smaller base. The tank's volume is 465 m3, the radii of the bases are 4 m and 3 m. Find the depth of the tank. - The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - The truncated The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
- Truncated pyramid
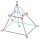The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Truncated pyramid
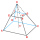Find the volume and surface area of a regular quadrilateral truncated pyramid if base lengths a1 = 17 cm, a2 = 5 cm, height v = 8 cm. - Truncated cone
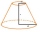Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm and side s = 10 cm. - Calculate 38701 Calculate the surface and volume of the cut rotating cone with base radii of 14cm and 8cm, height 11cm.
- Wooden bowls
20 wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has a d - Digging a pit
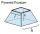The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14m and 10m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit? - Truncated cone 6
Calculate the volume of the truncated cone whose bases consist of an inscribed circle and a circle circumscribed to the opposite sides of the cube with the edge length a=1. - Equilateral cone
We pour so much water into a container that has the shape of an equilateral cone, the base of which has a radius r = 6 cm, that one-third of the volume of the cone is filled. How high will the water reach if we turn the cone upside down? - Cutting cone
A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm. - Truncated 12391
A sphere is inscribed into a truncated cone and touches both the base and the mantle. The base diameter of the cone is D. What is its diameter? - A concrete pedestal A concrete pedestal has a shape of a right circular cone having a height of 2.5 feet. The diameter of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the lateral surface area, total surface area, and the volume of the pedestal.
- Frustum of a cone
A reservoir contains 28.54 m³ of water when full. The diameter of the upper base is 3.5 m, while at the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Quadrilateral 5814
Calculate the surface area and volume of a regular quadrilateral truncated pyramid if the edges of the base are 87 cm and 64 cm and the wall height is 49 cm. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =?
Do you have homework that you can't solve? Ask a question, and we try to solve it.
