Fractions + area of a shape - practice problems
Number of problems found: 276
- A goat 2
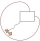 As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m².
As shown, a goat is tied at one corner of a rectangular shed by a 5-meter-long rope. The shed measures 3 m by 2 m and is surrounded by grassland. What is the area of the grassland in which the goat can graze? Give your answer to the nearest m². - Bradley
 Bradley is making a box that has a length of 14 7/8 inches and a width of 5 1/3 inches. How much wood does he need to make the box?
Bradley is making a box that has a length of 14 7/8 inches and a width of 5 1/3 inches. How much wood does he need to make the box? - A farmer 9
 A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes.
A farmer has 3 hectares of an orchard. ½ of the land is occupied by apples, ⅙ of the remainder is occupied by lemon trees, and tree tomatoes occupy the rest of it. Find the fraction of the land occupied by tree tomatoes. - Sonya
 Sonya, Jill, and Donna run each Monday. Jill ran 6/12 of an hour, and Donna ran 5/12 of an hour. If the girls ran a total of one whole hour, what fraction of an hour did Sonya run?
Sonya, Jill, and Donna run each Monday. Jill ran 6/12 of an hour, and Donna ran 5/12 of an hour. If the girls ran a total of one whole hour, what fraction of an hour did Sonya run? - Rectangle 83
 Rectangle land has a dimension of 8 km times 10 9/10 km. What is the area? Write your answer as a fraction or as a whole or mixed number.
Rectangle land has a dimension of 8 km times 10 9/10 km. What is the area? Write your answer as a fraction or as a whole or mixed number. - A room
 A room is 8 2/3 m by 5 1/4 m. What is the area of the room?
A room is 8 2/3 m by 5 1/4 m. What is the area of the room? - Nisha
 Nisha likes to make small rectangular paintings of cats. One of her paintings has an area of 33cm squared and a width of 7 1/2 centimeters. What is the height of this painting?
Nisha likes to make small rectangular paintings of cats. One of her paintings has an area of 33cm squared and a width of 7 1/2 centimeters. What is the height of this painting? - Linda
 Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first?
Linda gave her sister 2/5 of her money, spent 1/3, and saved the remainder. If Linda saved $28.00, how much money did she have at first? - An electorate
 In an electorate, 3/4 th of the voters are Tamils. Of the remaining 2/3 rd are Muslims, and the others are Sinhalese. If the number of Sinhalese in that electorate is 587, find the number of voters in that electorate.
In an electorate, 3/4 th of the voters are Tamils. Of the remaining 2/3 rd are Muslims, and the others are Sinhalese. If the number of Sinhalese in that electorate is 587, find the number of voters in that electorate. - The bedroom
 The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form.
The area of the rectangular bedroom is 136 5/8 square feet. If its width is 12 3/4 feet, find its length in simplest form. - Native plants
 In a garden, 5/6 of the area is filled with native plants. The native plants take up 107/4 m². Let g represent the total area of the garden. Find g = total area of the garden.
In a garden, 5/6 of the area is filled with native plants. The native plants take up 107/4 m². Let g represent the total area of the garden. Find g = total area of the garden. - A sandbox
 3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox?
3/4 a sandbox has an area of 20 square feet. The length is 6 1/2 feet. What is the width of the sandbox? - The playground 2
 The dome is built on the playground. The dome covers an area of 1 2/3 square meters, which is 5/840 of the total area of the playground. What is the total area of the playground?
The dome is built on the playground. The dome covers an area of 1 2/3 square meters, which is 5/840 of the total area of the playground. What is the total area of the playground? - A rectangle 13
 A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide?
A rectangle has an area of 15 square inches. What is the missing side length if one side length is 1 2/3 inches wide? - ET inscribed circle
 An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region.
An equilateral triangle has been inscribed in a circle with a radius of 4 cm . Find the area of the shaded region. - A bakery
 A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa
A bakery makes cylindrical mini muffins that measure 2 inches in diameter and one and one-fourth inches in height. If each mini muffin is completely wrapped in paper, then at least how much paper is needed to wrap 6 mini muffins? Approximate using pi equa - A frustum
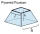 A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume.
A frustum of a pyramid consists of a square base of length 10 cm and a top square of length 7 cm. The height of the frustum is 6 cm. Calculate the surface area and volume. - Height of the box
 The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be?
The box needs to have a volume of 108 ¾ cubic inches. If the width of the box is going to be 7 ¼ inches, and depth of the box is going to be 1 ¼ inches, what must the height of the box be? - A park on map
 A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²?
A park has an area of ⅙ mi². On a map, the park has an area of 1 ¼ cm². On the map, how many square centimeters represent 1 mi²? - The plot
 Mr. Duma recently inherited a rectangular plot, part of the estate left by his late father. The plot with the following dimensions: Length=2x+1; Width=x-1. Determine the formula, in terms of x, that best describes the area of the rectangular plot. He has
Mr. Duma recently inherited a rectangular plot, part of the estate left by his late father. The plot with the following dimensions: Length=2x+1; Width=x-1. Determine the formula, in terms of x, that best describes the area of the rectangular plot. He has
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
