Geometry construction + Mathematical Olympiad - practice problems
Number of problems found: 10
- Book Store
 The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w
The Mabini Book Store (MBS) is reducing the prices of Mathematics books for promotion. The store has 6 Algebra books, 6 Geometry books, and 5 Statistics books to be arranged on a shelf. Books of the same kind are to be placed beside each other. How many w - Construct 11511
 Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options
Construct the diamond ABCD so that its diagonal BD is 8 cm and the distance of apex B from the line AD is 5 cm. Specify all options - Intersection 7247
 On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin
On side AB of triangle ABC, points D and E are given such that |AD| = |DE| = |EB|. Points A and B are the midpoints of segments CF and CG. Line CD intersects line FB at point I, and line CE intersects line AG at point J. Prove that the intersection of lin - Conditions 7186
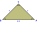 Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point
Given an isosceles right triangle ABS with base AB. On a circle centered at point S and passing through points A and B, point C lies such that triangle ABC is isosceles. Determine how many points C satisfy the given conditions and construct all such point - Isosceles - isosceles
 It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB.
It is given a triangle ABC with sides /AB/ = 3 cm /BC/ = 10 cm, and the angle ABC = 120°. Draw all points X such that the BCX triangle is an isosceles and triangle ABX is an isosceles with the base AB. - Z9–I–1
 In all nine fields of given shape to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in th
In all nine fields of given shape to be filled with natural numbers so that: • each of the numbers 2, 4, 6, and 8 is used at least once, • four of the inner square boxes containing the products of the numbers of adjacent cells of the outer square, • in th - Mrak - cloud
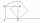 It is given segment AB of length 12 cm, where one side of the square MRAK is laid on it. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB the point R leaves a paper trail. Draw the whole track of point R until the square ca
It is given segment AB of length 12 cm, where one side of the square MRAK is laid on it. MRAK's side length is 2 cm shown. MRAK gradually flips along the line segment AB the point R leaves a paper trail. Draw the whole track of point R until the square ca - Hexagon - MO
 The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and is true |DJ|
The picture shows the ABCD square, the EFGD square, and the HIJD rectangle. Points J and G lie on the side CD and is true |DJ| - Katy MO
 Kate drew a triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4
Kate drew a triangle ABC. The middle of the line segment AB has marked as X and the center of the side AC as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4 - Square grid
 A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid.
A square grid consists of a square with sides of a length of 1 cm. Draw at least three patterns, each with an area of 6 cm² and a circumference of 12 cm, and their sides in a square grid.
We apologize, but in this category are not a lot of examples.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
Do you have homework that you need help solving? Ask a question, and we will try to solve it.
